1. 摘要

这篇文章^[1]提出了一个参数化的非线性变换(GDN, Generalized Divisive Normalization)，用来高斯化图像数据（高斯化图像数据有许多好处，比如方便压缩）。整个非线性变换的架构为：数据首先经过线性变换，然后通过合并的活动度量对每个分量进行归一化（这个活动度量是对整流和取幂分量的加权和一个常数进行取幂计算）。作者利用负熵度量对整个非线性变换进行优化。优化后的变换高斯化数据的能力得到很大提升，并且利用该变换得到的输出分量之间的互信息要远小于其它变换（比如独立成分分析 ICA 和径向高斯化 RG）。整个非线性变换是可微的，同时也可以有效地逆转，从而得到其对应的逆变换，二者一组合就得到了一个端到端的图像密度模型。在这篇文章中，作者展示了这个图像密度模型处理图像数据的能力（比如利用该模型作为先验概率密度来移除图像噪声）。此外，这个非线性变换及其逆变换都是可以级连的，每一层都使用同样的高斯化目标函数。最后，本文提出的 GDN 可以用来估计自然图像的概率分布，因此提供了一种用于优化神经网络的无监督方法。

2. 引言

近年来，用于复杂模式分类的表示学习取得了很大的进步。然而，大多数表示学习方法都是有监督的，而现实中标签数据往往可欲而不可求，因此能否找到以及如何找到无监督的表示学习方法成为了一个重要问题。概率密度估计是所有无监督学习的基石。

一个直接的想法是通过拟合数据得到概率密度模型，该模型要么来自参数族，要么由内核的非参数叠加组成。另一个间接的方法是寻求一个可逆且可微的参数化函数 $\boldsymbol{y} = g(\boldsymbol{x}; \boldsymbol{\theta})$ 来将数据映射到到一个固定的目标概率密度模型 $p_{\boldsymbol{y}}(\boldsymbol{y})$ ，这个目标概率密度模型的原像则为输入空间提供了一个概率密度模型。这种间接的方法既能够得到不同概率密度族的模型，而且在某些情况下更容易优化。

以下是作者在文中提到的一些无监督学习方法：

无监督学习方法	论文出处
PCA(Principal Component Analysis)	Jolliffe, 2002<span class="hint--top hint--rounded" aria-label="Jolliffe, I. T. Principal Component Analysis. Springer, 2 edition, 2002. ISBN 978-0-387-95442-4.
">[2]
ICA(Independent Component Analysis)	Cardoso, 2003<span class="hint--top hint--rounded" aria-label="Cardoso, Jean-François. Dependence, correlation and Gaussianity in independent component analysis. Journal of Machine Learning Research, 4:1177–1203, 2003. ISSN 1533-7928.
">[3]
RG(Radial Gaussianization)	Lyu & Simoncelli, 2009b<span class="hint--top hint--rounded" aria-label="Lyu, Siwei and Simoncelli, Eero P. Nonlinear extraction of independent components of natural images using radial Gaussianization. Neural Computation, 21(6), 2009b. doi: 10.1162/neco. 2009.04-08-773.
">[4] Sinz & Bethge, 2010<span class="hint--top hint--rounded" aria-label="Sinz, Fabian and Bethge, Matthias. Lp-nested symmetric distributions. Journal of Machine Learning Research, 11:3409–3451, 2010. ISSN 1533-7928.
">[5]

对于 ICA 方法，可以应用非参数的非线性到线性数据的边缘密度上来实现对数据的高斯化。即 ICA-MG(ICA-Marginal-Gaussianization) 方法。

在这篇文章中，作者定义了一种泛化的分裂归一化(DN, Divisible Normalization^[6])变换方法，其可以特化为 ICA-MG 或 RG 方法。作者通过优化变换后数据的非高斯性的无监督学习目标来优化该变换的参数。GDN 是连续且可微的，并且作者给出了其逆变换的有效方法。作者表示，GDN 能够对局部过滤器输出的成对数据产生更好的拟合效果，并生成更加自然的图像块（因此可以用于图像处理问题，比如图像去噪）。此外，两层级联的 GDN 变换在捕获图像统计数据上效果更好。更广泛地来说，GDN 可以当作一个一般的深度无监督学习工具。

3. 数据高斯化

给定一个变换参数族 $\boldsymbol{y} = g(\boldsymbol{x}; \boldsymbol{\theta})$，我们希望选择合适的参数 $\boldsymbol{\theta}$ 来将输入向量 $\boldsymbol{x}$ 变换成标准的正态随机向量。若 $g$ 是可微变换，则输入 $\boldsymbol{x}$ 和输出 $\boldsymbol{y}$ 之间的关系为：

$$p_{\boldsymbol{x}}(\boldsymbol{x}) = \left\lvert \frac{\partial g(\boldsymbol{x}; \boldsymbol{\theta})}{\partial \boldsymbol{x}}\right\rvert \ p_{\boldsymbol{y}}(g(\boldsymbol{x}; \boldsymbol{\theta})) \tag{1}$$

其中 $\lvert \cdot \rvert$ 表示对矩阵行列式取绝对值。如果 $p_{\boldsymbol{y}}$ 是标准的正态分布，即 $\mathcal{N}(0, 1)$，那 $p_{\boldsymbol{x}}$ 的形状则完全只由变换 $g$ 决定。换句话来说，$g$ 诱导了一个 $\boldsymbol{x}$ 上的概率密度模型，其由参数 $\boldsymbol{\theta}$ 确定。我们需要求解的即为参数 $\boldsymbol{\theta}$。

此时，当给定 $p_{\boldsymbol{x}}$ 或者是从 $p_{\boldsymbol{x}}$ 采样得到的数据，概率密度估计问题可以通过最小化变换 $\boldsymbol{y}$ 的概率密度和正态分布之间的 KL 散度来求解，即负熵度量：

\begin{align*} J(p_{\boldsymbol{y}}) & = \mathbb{E}_{\boldsymbol{y}} (\log{p_{\boldsymbol{y}}}(\boldsymbol{y}) - \log{\mathcal{N}(\boldsymbol{y})}) \\ & = \mathbb{E}_{\boldsymbol{x}} \left(\log{p_{\boldsymbol{x}}}(\boldsymbol{x}) - \log{\left\lvert \frac{\partial g(\boldsymbol{x};\boldsymbol{\theta})}{\partial \boldsymbol{x}} \right\rvert} - \log{\mathcal{N}(g(\boldsymbol{x}; \boldsymbol{\theta}))}\right) \tag{2} \end{align*}

对 $\boldsymbol{\theta}$ 求导后，得

\begin{align*} \frac{\partial J(p_{\boldsymbol{y}})}{\partial \boldsymbol{\theta}} = \mathbb{E}_{\boldsymbol{x}} \left( -\sum_{ij} \left[ \frac{\partial g(\boldsymbol{x}; \boldsymbol{\theta})}{\partial \boldsymbol{x}} \right]_{ij}^{-T} \frac{\partial^2 g_i(\boldsymbol{x}; \boldsymbol{\theta})}{\partial x_j \partial \boldsymbol{\theta}} + \sum_{i} g_i(\boldsymbol{x}; \boldsymbol{\theta}) \frac{\partial g_i(\boldsymbol{x}; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \right) \tag{3} \end{align*}

这里的求导需要矩阵微分的相关知识，就不展开了。证明的话有个难点就是要用到迹的一个性质：$\mathrm{tr}(A^\top B) = \sum_{ij} A_{ij} B_{ij}$。

需要注意的是，虽然根据式 $(3)$ 进行梯度优化 $\boldsymbol{\theta}$ 是可行的，但现实很难求出公式 $(2)$ 对应的 KL 散度，因为它需要对 $p_{\boldsymbol{x}}$ 的熵进行估计。这里作者给出的替代方案是计算输出负熵和输入负熵之间的差值：

$$\Delta J \equiv J(p_{\boldsymbol{y}}) - J(p_{\boldsymbol{x}}) = \mathbb{E}_{\boldsymbol{x}} \left( \frac{1}{2} \lVert \boldsymbol{y} \rVert_2^2 - \log{\left\lvert \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} \right\rvert - \frac{1}{2} \lVert \boldsymbol{x} \rVert_2^2} \right) \tag{4}$$

式 $(4)$ 给出了变换后的数据 $\boldsymbol{y}$ 相对于变换前的数据 $\boldsymbol{x}$ 高斯化的程度。

由于负熵是非负的，且越小表示越接近标准正态分布，因此 $\Delta J$ 负的越多表示变换 $g$ 高斯化效果越好。

4. 分裂归一化

分裂归一化是一种增益控制方法，其已经成为描述感觉神经元非线性特性的标准模型。分裂归一化的定义如下：

$$y_i = \gamma \frac{x_i^\alpha}{\beta^\alpha + \sum_j x_j^\alpha} \tag{5}$$

其中，$\boldsymbol{\theta} = \{\alpha, \beta, \gamma\}$ 为参数。大致来说，分裂归一化成功将输入 $\boldsymbol{x}$ 中每个元素的值调整到一个目标范围，同时保持了它们之间的相对大小关系。这个方法常常用在一些高斯模型中（比如 GSM），用来高斯化数据，同时其也存在诸多改版。然而，很多改版都具有或多或少的局限性，故作者在本文中给出了一个更为一般的泛化版本，其定义如下：

\begin{align*} \boldsymbol{y} = g(\boldsymbol{x};\boldsymbol{\theta}) && \text{ s.t. } &&& y_i = \frac{z_i}{(\beta_i + \sum_j \gamma_{ij} |z_j|^{\alpha_{ij}})^{\varepsilon_i}}\\ && \text{ and } &&& \boldsymbol{z} = \boldsymbol{H} \boldsymbol{x} \tag{6} \end{align*}

其中，全参数向量 $\boldsymbol{\theta}$ 包含向量 $\boldsymbol{\beta}$ 和 $\boldsymbol{\varepsilon}$ 以及矩阵 $\boldsymbol{H}, \boldsymbol{\alpha}, \boldsymbol{\gamma}$，总共 $2N + 3N^2$ 个参数（$N$ 为输入数据维度）。作者将式 $(6)$ 称为 GDN(Generalized Divisive Normalization)，因为它泛化了最初的分裂归一化模型及其许多改版。

为了让式 $(6)$ 对应的变换能够使用第 [3](## 3. 数据高斯化) 节的优化方法，需要保证 $(6)$ 对应的变换是连续可微的，且此外还要求其雅可比矩阵可逆（见式 $(3)$）。首先保证 $(6)$ 对应的变换是连续可微的，由于式 $(6)$ 分为两部分，第二部分 $\boldsymbol{z} = \boldsymbol{H} \boldsymbol{x}$ 显然是连续可微的，而第一部分求偏导得：

$$\frac{\partial y_i}{\partial z_k} = \frac{\delta_{ik}}{(\beta_i + \sum_j \gamma_{ij} |z_j|^{\alpha_{ij}})^{\varepsilon_i}} - \frac{\alpha_{ik} \gamma_{ik} \varepsilon_i z_i |z_k|^{\alpha_{ik} - 1} \mathrm{sgn}(z_k)}{(\beta_i + \sum_j \gamma_{ij} |z_{j}|^{\alpha_{ij}})^{\varepsilon_i + 1}} \tag{7}$$

要保证连续性，则要求上述偏导对所有的 $\boldsymbol{z} \in \mathbb{R}^N$ 都是有限的。因此作者在这里要求上式中所有的指数是非负的且分母括号中的表达式是正的，这样就能确保上述偏导对所有的 $\boldsymbol{z} \in \mathbb{R}^N$ 始终都是有限的。此时要求的条件为：$\beta_i > 0, \gamma_{ij}, \varepsilon_i \geq 0, \alpha_{ij} \geq 1$。

这里作者给出的应该只是充分条件，而不是充要条件，具体证明证不来。@_@

然后来保证保证 $(6)$ 对应变换的雅可比矩阵可逆。根据矩阵微分的链式法则（个人采用分母布局）：

$$\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}} \cdot \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{z}} \tag{8}$$

故 $J_{\boldsymbol{y} \rightarrow \boldsymbol{x}} = J_{\boldsymbol{z} \rightarrow \boldsymbol{x}} \cdot J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$，其中 $J_{\boldsymbol{y} \rightarrow \boldsymbol{x}}$ 表示 $\boldsymbol{y}$ 对 $\boldsymbol{x}$ 的雅可比矩阵，其它的以此类推。要保证 $J_{\boldsymbol{y} \rightarrow \boldsymbol{x}}$ 可逆，也即非奇异，则要求雅可比行列式 $|J_{\boldsymbol{y} \rightarrow \boldsymbol{x}}| \neq 0$。根据行列式的性质，即要求 $|J_{\boldsymbol{z} \rightarrow \boldsymbol{x}}| \cdot |J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}| \neq 0$，从而要求 $|J_{\boldsymbol{z} \rightarrow \boldsymbol{x}}| \neq 0$ 且 $|J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}| \neq 0$。

• 对于 $|J_{\boldsymbol{z} \rightarrow \boldsymbol{x}}| \neq 0$，即 $|H| \neq 0$，也即要求参数矩阵 $H$ 非奇异即可；

• 对于 $|J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}| \neq 0$，作者给出了一个充分条件，即让 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 正定，这个最终是通过在初始化参数时保证的。此外，为了方便求解式 $(6)$ 变换的逆，作者要求单变量映射 $y_i \rightarrow z_i$ 是可逆的，根据式 $(6)$ 有：

  $$|y_i| = \frac{|z_i|}{(\beta_i + \sum_{j} \gamma_{ij} |z_j|^{\alpha_{ij}})^{\varepsilon_i}} \leq \frac{|z_i|}{\gamma_{ii}^{\varepsilon_i} |z_i|^{\alpha_{ii} \varepsilon_i}} = \gamma_{ii}^{-\varepsilon_i} |z_i|^{1-\alpha_{ii} \varepsilon_i} \tag{9}$$

  由于单变量映射 $y_i \rightarrow z_i$ 连续可逆，因此 $y_i$ 关于 $z_i$ 一定得是单调的，从而要求 $1 - \alpha_{ii} \varepsilon_i \geq 0$，即 $\varepsilon_i \leq \alpha_{ii}^{-1}$。

综合上述的讨论，最终的参数条件为：$\alpha_{ij} \geq 1, \beta_i > 0, \gamma_{ij} \geq 0, 0 \leq \varepsilon_i \leq \alpha_{ii}^{-1}$，并且在最初初始化模型时，保证雅可比矩阵 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 是正定的。

作者在文章中给的一个方法是设定参数矩阵 $\boldsymbol{\gamma}$ 是对角的，这样式 $(7)$ 就化简为：

$$\frac{\partial y_i}{\partial z_k} = \begin{cases} 0 & i \neq k \\ \frac{\beta_i + \gamma_{ii}|z_i|^{\alpha_{ii}}(1 - \alpha_{ii} \varepsilon_i \mathrm{sgn}(z_i))}{(\beta_i + \gamma_{ii} |z_i|^{\alpha_{ii}})^{\varepsilon_i + 1}} & i = k \end{cases}$$

显然雅可比矩阵 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}} = \frac{\partial y_i}{\partial z_k}$ 也是对角的，且主对角上的元素均大于 $0$。

但是，只是在初始化参数的时候保证雅可比矩阵 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 是正定的还不够，因为在优化过程中它可能变得不正定。由于变换 $\boldsymbol{y} \rightarrow \boldsymbol{z}$ 是连续的，因此如果在优化过程中 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 变得不再正定，则说明当优化步长足够小时，至少存在某个点，$J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 的某个特征值变成 $0$，此时 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 变得奇异了。根据优化的负熵度量公式 $(2)$ ，当 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 奇异时，项 $-\log{\lvert \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} \rvert}$ 会变成无穷大，因此这个惩罚项使得不可能出现上述的情况。也就是说，一旦设定好初始值使得 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 正定后，使用负熵度量进行优化时，在优化过程中是不会改变 $J_{\boldsymbol{y} \rightarrow \boldsymbol{z}}$ 的正定性的。

最后，作者还给出了求变换 $\boldsymbol{y} \rightarrow \boldsymbol{z}$ 逆的定点迭代方法：

$$z_i^{(0)} = \mathrm{sgn}(y_i) (\gamma_{ii}^{\varepsilon_i} |y_i|)^{\frac{1}{1 - \alpha_{ii}\varepsilon_i}} \\ z_i^{(n+1)} = \left( \beta_i + \sum_j \gamma_{ij} |z_j^{(n)}|^{\alpha_{ij}} \right)^{\varepsilon_i} y_i \tag{10}$$

该定点迭代方法的收敛性证明……证不来@_@

5. 实验

优化 GDN 模型的体现就在于能否学习到自然图像数据的分布。作者针对式 $(3)$ 提出的梯度使用 SGD 方法来优化整个模型的参数。

5.1 小波系数对

作者对比了其提出的 GDN 模型和 ICA、RG 模型，在估计图像小波系数对的联合概率密度上的效果。作者首先使用方向可控金字塔的小波过滤器对图像进行预处理，图像数据集采用的是 van Hateren，然后通过设置不同的空间域偏移 $d$ 来得到成对的子带系数，也即形成了一个二维的数据集。最后再分别用 ICA、RG 和 GDN 模型对产生的一系列成对子带系数进行变换，变换后的二维数据间的互信息如下图所示：

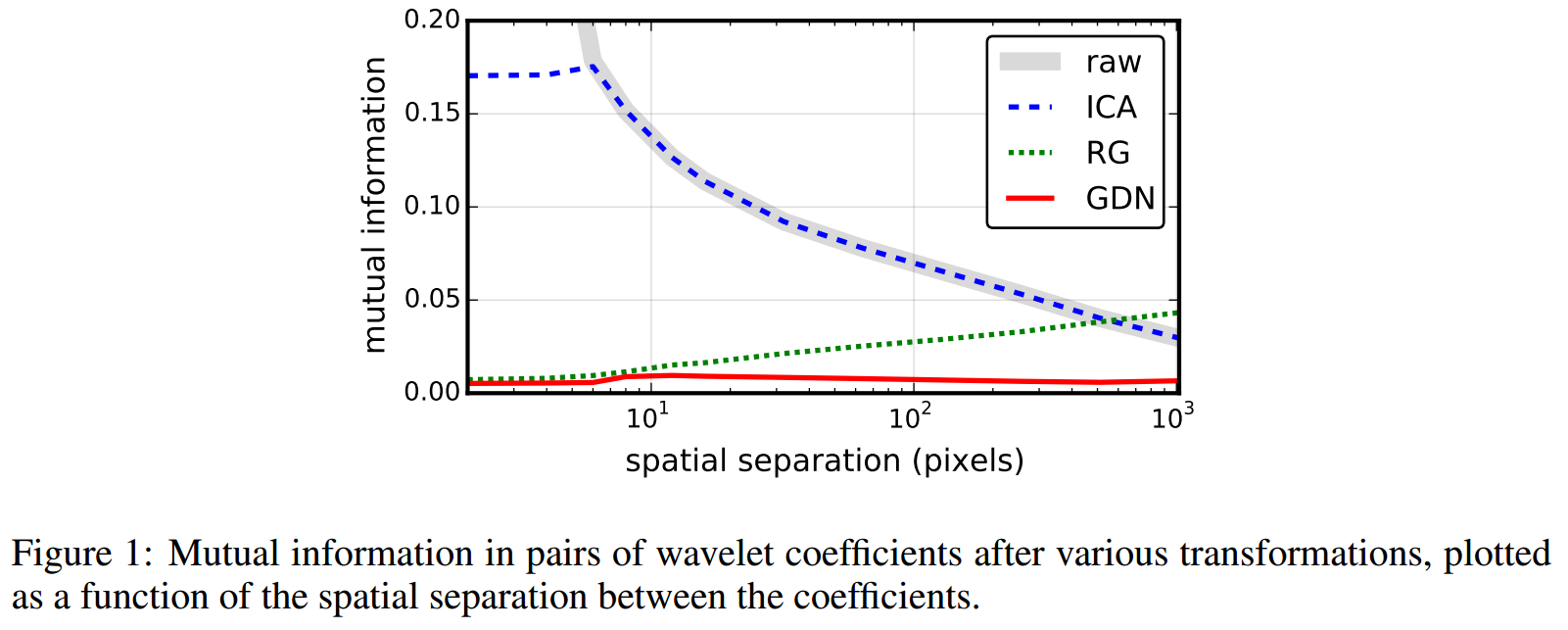
其中，横坐标表示的是空间域偏移 $d$，纵坐标表示的是互信息。可以看到，无论 $d$ 取值多大，GDN 模型变换后的数据互信息都很小，也即变换后的数据之间只有很小的相关性。而 ICA 模型和 RG 模型都只是在 $d$ 取值较大或较小时才表现出很好的去相关效果。

作者说在这里互信息通过一个加性常数和式 $(2)$ 表示的负熵相关。不是很理解……

根据互信息的定义：

\begin{align*} I(y_1, y_2) & = \mathrm{DL}(p(y_1, y_2) \parallel p(y_1) \otimes p(y_2)) \\ & = \mathbb{E}_{\boldsymbol{y}} \log{\left( \frac{p_{\boldsymbol{y}}(\boldsymbol{y})}{p_{y_1}(y_1) p_{y_2}(y_2)} \right)} \\ & = \mathbb{E}_{\boldsymbol{y}} \log{p_{\boldsymbol{y}}(\boldsymbol{y})} - \mathbb{E}_{y_1} \log{p_{y_1}(y_1)} - \mathbb{E}_{y_2} \log{p_{y_2}(y_2)} \end{align*}

多出来的 $- \mathbb{E}_{y_1} \log{p_{y_1}(y_1)} - \mathbb{E}_{y_2} \log{p_{y_2}(y_2)}$ 和式 $(2)$ 中的 $-\mathbb{E}_{\boldsymbol{y}} (\log{\mathcal{N}(\boldsymbol{y})})$ 有常数关系吗？迷茫……如果有大佬知道这里怎么理解希望告诉我一下 @_@

同时，作者还对比了 ICA、RG 和 GDN 模型估计变换前数据分布的效果。作者使用非参数估计中的直方图估计作为参照，然后根据式 $(1)$ 计算出模型拟合的分布，并对比其和参照的差异，如下图所示：

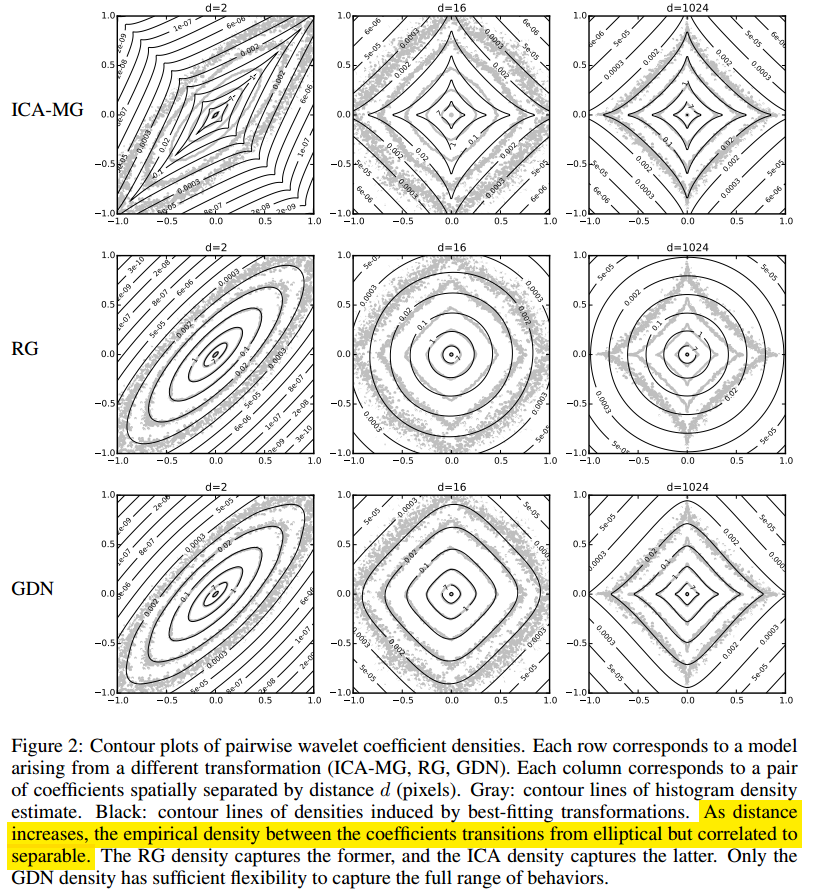
其中，实线表示模型估计的拟合分布，灰色散点图表示直方图估计的分布。可以看到，GDN 对于所有范围的 $d$ 值给出的拟合分布都和直方图估计给出的大致一致，而 ICA-MG 和 RG 都只是在 $d$ 取值较大或较小时才表现出很好的估计效果。

5.2 图像块

作者还对比了不同模型在估计图像块像素的联合密度上的效果。这里，作者从 Kodak 数据集上裁取 $16 \times 16$ 的图像块，然后使用 Adam 优化方法来优化不同模型。同时为了减小模型的复杂度，作者在这里限制了 $\alpha_{ij} \equiv \alpha_j$。由于是 $256$ 维的高维数据， 很难给出可视化效果，因此作者在一些度量上进行了比较：

5.2.1 负熵减少量

正如式 $(4)$ 所说那样，可以用 $\Delta J$ 来衡量模型的高斯化效果。负熵减少量越大，表示高斯化效果越好，估计 $\boldsymbol{x}$ 的分布也就越准。经过实验，ICA-MG 和 RG 的负熵减少量分别为 $2.04$ nats（即 $\Delta J = -2.04$ nats）和 $2.11$ nats，而 GDN 的负熵减少量为 $2.43$ nats。

5.2.2 变换数据的边缘分布和径向分量分布

如果变换后的数据是多维标准正态分布，那么变换后数据的边缘分布应该也是标准正态分布，且其径向分量应该符合度为 $256$ 的卡方分布。

多维随机变量 $\boldsymbol{y}$ 的径向分量为 $z = \left\lVert \boldsymbol{y} \right\rVert_2 = \sqrt{\sum_{i} y_i^2}$。

于是作者给出了 ICA-MG、RG 和 GDN 的变换数据的边缘分布和径向分量分布对比图，如下所示：

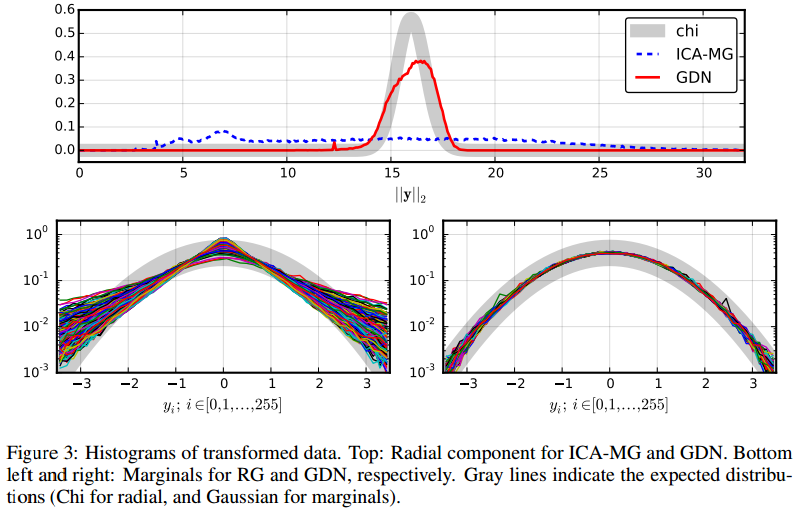
可以看到，GDN 模型在边缘分布和径向分量分布上都表现得要好于 ICA-MG 和 RG 模型。ICA-MG 在径向分量分布上很差而 RG 模型在边缘分布上很差。

5.2.3 采样

作者提出，衡量高斯化变换模型的另一种可视化方法是，当假定变换得到的数据是符合多维标准正态分布时，通过对标准正态分布数据使用逆变换进行采样得到图像像素数据，并对比其和自然图像，如下图所示：

作者给出了从数据集采集的部分自然图像块，和分别采用 ICA-MG 和 GDN 模型逆变换得到的标准正态分布的采样图像块。可以看到，ICA-MG 模型给出的图像块非常紊乱不自然，GDN 要相对好一些。

5.2.4 去噪

作者给出另一种衡量模型估计未知数据分布的能力，即使用模型估计的分布作为一种先验用在图像去噪中。这里作者考虑加性高斯噪声，并使用经验贝叶斯解公式由估计的噪声数据分布 $p_{\tilde{\boldsymbol{x}}}$ 推导得到原图像的数据分布，经验贝叶斯解公式如下：

$$\hat{\boldsymbol{x}} = \tilde{\boldsymbol{x}} + \sigma^2 \nabla \log{p_{\tilde{\boldsymbol{x}}}} (\tilde{\boldsymbol{x}})$$

其中，$\tilde{\boldsymbol{x}}$ 是噪声图像数据，$\sigma^2$ 是 $\tilde{\boldsymbol{x}}$ 的方差，$\hat{\boldsymbol{x}}$ 是使用经验贝叶斯推断得到的最优估计。虽然 GDN 模型是提出用来建模自然图像的分布的，但由于加上了可加高斯噪声， 作者发现 GDN 模型也能很好地建模（不愧是 Generalized Divisive Normalization）。为了对比去噪效果，作者使用了另外两种方法作为对照，一个是 marginal model^[7]，另一个是 GSM^[8] 模型，这两个方法都是在正交小波系数据进行图像去噪的。最后给出的去噪可视化效果及 PSNR 和 SSIM 指标得分如下图所示：

5.2.5 平均对数似然

进一步了解这块可能需要先看看另一篇文章^[9]。

为了进一步评估 GDN 模型的有效性，作者对比了另一篇文章^[9]中提到的一些图像生成模型及其评价方法。这里作者沿用文章^[9]的设置，使用 BSDS300 数据集，并将图像切分为 $8 \times 8$ 的图像块。然后对图像块进行建模，并计算模型给出的图像块中像素的对数似然及平均每个像素的对数似然（越大表示估计的越准）。需要注意的是，作者在这里进行了一些预处理，即移除图像块的平均值。作者发现 GDN 模型给出的平均对数似然为 $151.5$ nats，而 ICA-MG 模型给出的平均对数似然为 $126.8$ nats，但都比不过文章^[9]给出的最优的 MCGSM 模型。另一方面，作者发现如果不移除图像块的平均值，则 GDN 可以达到和最优的 MCGSM 模型一样的性能。

5.3 两层级联

作者在实验中发现，GDN 模型能很好地建模局部小范围的图像块，但当图像块范围扩大时，GDN 的性能就开始会下降，即无法捕获大范围的图像块像素间的统计关系。作者这里给出的解决办法是级联两层 GDN 来获得更大的捕获范围。一般的高斯化变换级联都会在每一层上加上一下线性变换层，用来旋转前面输出的数据以暴露出还未高斯化的维度，从而尽可能地让数据的所有维度都高斯化。这里也一样，不过作者选择了 CICA^[10] 而不是线性变换作为中间层来旋转数据，最后的级联结构为：CICA-GDN-CICA-GDN。此时作者使用了 $48 \times 48$ 大小的图像块作为输入，最后给出的变换后数据的边缘分布如下图所示：

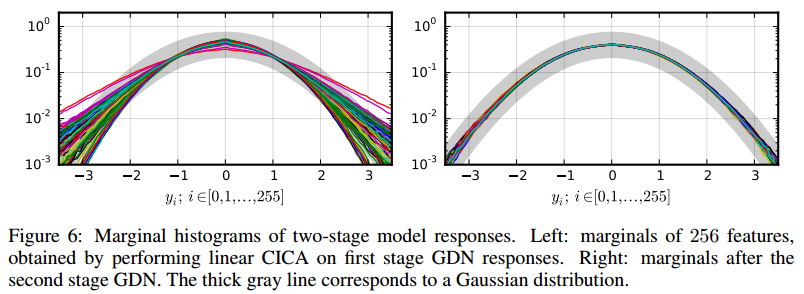
其中，左边为第一层的 CICA-GDN 的输出结果，右边为第二层的 CICA-GDN 的输出效果。可以看到，第二层的 CICA-GDN 在第一层的基础上对那些未成功高斯化的维度进行了进一步的高斯化，最后达到了较好的边缘高斯化效果。

6. 总结

作者提出了一种新的概率模型 GDN 用来建模自然图像，GDN 被隐式定义为一种可逆非线性变换，该变换经过优化，可以对数据进行高斯化。同时作者也给出了优化 GDN 的方法（即优化负熵）。作者在数据高斯化、去噪及采样方面验证了 GDN 的有效性。

个人总结：Balle 大佬的文章，无论在深度和广度上都大大震憾到我了，啃这篇文章前前后后花了我 2-3 周的时间，不过也收获满满。如果也有做可学习图像压缩方向的小伙伴，强烈建议认真读一读 Balle 大佬的系列文章。最后，希望本文也能给各位小伙伴带来一些收获吧～

本人能力有限，如果文中有表述不对的地方还希望大家能及时指出，谢谢啦～

附录

1. Ballé, J., Laparra, V., & Simoncelli, E. P. (2016, January). Density modeling of images using a generalized normalization transformation. In 4th International Conference on Learning Representations, ICLR 2016. ↩
2. Jolliffe, I. T. Principal Component Analysis. Springer, 2 edition, 2002. ISBN 978-0-387-95442-4. ↩
3. Cardoso, Jean-François. Dependence, correlation and Gaussianity in independent component analysis. Journal of Machine Learning Research, 4:1177–1203, 2003. ISSN 1533-7928. ↩
4. Lyu, Siwei and Simoncelli, Eero P. Nonlinear extraction of independent components of natural images using radial Gaussianization. Neural Computation, 21(6), 2009b. doi: 10.1162/neco. 2009.04-08-773. ↩
5. Sinz, Fabian and Bethge, Matthias. Lp-nested symmetric distributions. Journal of Machine Learning Research, 11:3409–3451, 2010. ISSN 1533-7928. ↩
6. Heeger, David J. Normalization of cell responses in cat striate cortex. Visual Neuroscience, 9(2), 1992. doi: 10.1017/S0952523800009640. ↩
7. Figueiredo, M. A. T. and Nowak, R. D. Wavelet-based image estimation: an empirical bayes approach using Jeffrey’s noninformative prior. IEEE Transactions on Image Processing, 10(9), September 2001. doi: 10.1109/83.941856. ↩
8. Portilla, Javier, Strela, Vasily, Wainwright, Martin J., and Simoncelli, Eero P. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Transactions on Image Processing, 12 (11), November 2003. doi: 10.1109/TIP.2003.818640. ↩
9. Theis, Lucas and Bethge, Matthias. Generative image modeling using spatial LSTMs. In Advances in Neural Information Processing Systems 28, pp. 1918–1926, 2015. ↩
10. Ballé, Johannes and Simoncelli, Eero P. Learning sparse filterbank transforms with convolutional ICA. In 2014 IEEE International Conference on Image Processing (ICIP), 2014. doi: 10.1109/ICIP.2014.7025815. ↩