2016-PCS-End-to-end optimization of nonlinear transform codes for perceptual quality

1. 摘要

这篇文章[1]提出了一个通用的变换编码框架，用于提升假定使用标量量化的端到端的非线性变换编码的率失真性能。结合任意可微的感知度量，这个框架可以用于优化任意可微的分析变换和综合变换对。

2. 变换编码框架

这篇文章提出的变换编码框架的可视化如下图所示：

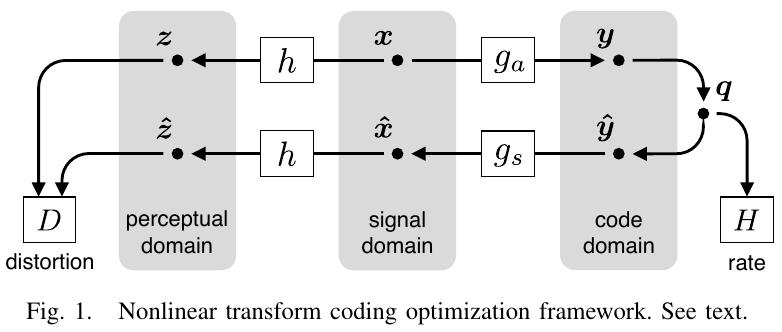
2.1 编解码流程

编码时，图像向量 x\boldsymbol{x} 经过可微变换 gag_a 得到编码向量 y=ga(x;ϕ)\boldsymbol{y} = g_a(\boldsymbol{x};\boldsymbol{\phi})，其中 ϕ\boldsymbol{\phi} 向量用来参数化可微变换 gag_a。然后对编码向量 y\boldsymbol{y} 进行标量量化，即得到量化指数 q\boldsymbol{q}，用于最终的编码存储。解码时，根据量化指数 q\boldsymbol{q}，可以反量化得到解码向量 y^\hat{\boldsymbol{y}}，y^\hat{\boldsymbol{y}} 经过可微的反变换 gsg_s 得到重建图像向量 x^\hat{\boldsymbol{x}}，其中 θ\boldsymbol{\theta} 向量用来参数化可微变换 gsg_s。

【注】该框架不仅仅局限于优化常见的线性变换，可微变换 gag_a 和 gsg_s 可以是线性的也可以是非线性的。在机器学习中，自编码器很适合充当这个非线性变换对。

2.2 率失真评估

  • 码率通过测量量化指数 q\boldsymbol{q} 的概率分布 PqP_{\boldsymbol{q}} 来评估。
  • 经典情况下，失真是通过计算 x\boldsymbol{x} 和 x^\hat{\boldsymbol{x}} 之间的 MSE（或等价的 PSNR）来评估的；然而，MSE（或 PSNR）和人眼视觉的感知不是完全一致的，MSE 衡量的是信号域上的失真，而人眼感知的是视觉感知域上的失真。因此，为了优化失真评估，作者在这里框架中引进了感知变换 hh，通过先将信号数据变换了感知数据，再来计算二者间的失真；即先计算 z=h(x)\boldsymbol{z} = h(\boldsymbol{x}) 和 z^=h(x^)\hat{\boldsymbol{z}} = h(\hat{\boldsymbol{x}}) ，然后使用一个比较好的范数来计算 z\boldsymbol{z} 和 z^\hat{\boldsymbol{z}} 之间的失真。

由于我们需要优化的是图像信号的编解码，因此 hh 不是我们要优化的目标，我们要优化的目标是 gag_a、gsg_s（具体而言即 {ϕ,θ}\{\boldsymbol{\phi}, \boldsymbol{\theta}\}）和标量量化器，但标量量化器一般是确定不变的且不可微的。所以这篇只考虑优化 {ϕ,θ}\{\boldsymbol{\phi}, \boldsymbol{\theta}\}，最终要优化的率失真函数如下：

L[ga,gs]=H[Pq]+λE∥z−z^∥(1)L[g_a, g_s] = H[P_{\boldsymbol{q}}] + \lambda \mathbb{E} \parallel \boldsymbol{z} - \hat{\boldsymbol{z}} \parallel \tag{1}

3. 近似标量量化

针对要优化的率失真函数 (1)(1)，其等号右边的两项都依赖于量化指数 q\boldsymbol{q}，但标量量化器都是不可微的，因此率失真函数 L[ga,gs]L[g_a, g_s] 也是不可微的，无法直接用于数值优化。为此，作者提出了一种近似标量量化的方法。

  • 不失一般性，首先假定所用的标量量化器为均匀的，且量化区间为 11。

    对于量化区间不为 11 的，我们可以通过调整分析变换和综合变换的系数来缩放量化区间到 11；对于非均匀量化，我们可以通过压缩扩展来将其转变为均匀量化。

    均匀量化器作用于 y\boldsymbol{y} 中的每一个元素，用数学公式描述为 y^i=round(yi)\hat{y}_i = \mathrm{round}(y_i)，其对应的边缘概率密度函数可表示为：

    py^i(t)=∑n=−∞∞Pqi(n)δ(t−n)(2)p_{\hat{y}_i}(t) = \sum_{n=-\infty}^{\infty} P_{q_i}(n) \delta(t-n) \tag{2}

    其中 Pqi(n)=(pyi∗rect)(n),∀n∈ZP_{q_i}(n) = (p_{y_i} * \mathrm{rect})(n), \forall n \in \mathbb{Z}，表示 yiy_i 量化为整数值 nn 对应的概率。δ\delta 为狄拉克函数，pyip_{y_i} 为 yiy_i 的边缘密度函数，rect\mathrm{rect} 为 (−12,12)(-\frac{1}{2},\frac{1}{2}) 上的均匀分布的概率密度函数，pyi∗rectp_{y_i}*\mathrm{rect} 表示二者做卷积，具体形式为：

    (pyi∗rect)(n)=∫−∞∞pyi(n−x)⋅rect(x)dx=∫−1212pyi(n−x)dx(p_{y_i} * \mathrm{rect})(n) = \int_{-\infty}^{\infty} p_{y_i}(n-x) \cdot \mathrm{rect}(x) dx = \int_{-\frac{1}{2}}^{\frac{1}{2}} p_{y_i}(n-x) dx

    卷积有两种形式，二者是等价的：p∗q=∫−∞∞p(x)q(t−x)dx=∫−∞∞p(t−x)q(x)dx=q∗pp * q = \int_{-\infty}^{\infty} p(x) q(t-x) dx = \int_{-\infty}^{\infty} p(t-x) q(x) dx = q * p。

    这也是符合我们的直观理解的，即量化区间为 11 的均匀量化器会将区间 (n−12,n+12)(n-\frac{1}{2}, n+\frac{1}{2}) 范围内的实数都量化为 nn，故 yiy_i 量化为整数 nn 的概率为 ∫−1212pyi(n−x)dx\int_{-\frac{1}{2}}^{\frac{1}{2}} p_{y_i}(n-x) dx，如此即得到 y^i\hat{y}_i 的所有离散概率值 Pqi(n),∀n∈ZP_{q_i}(n), \forall n \in \mathbb{Z}，也即可以进一步得到 y^i\hat{y}_i 的累积概率分布。已知 y^i\hat{y}_i 的累积概率分布，则 y^i\hat{y}_i 的概率密度函数可证明即为式 (2)(2)。

    为了方便理解，我们考虑 yiy_i 量化为区间 (−∞,t](-\infty, t] 中的任意一个整数的概率，我们从直观上可以直接给出答案，即 ∑n=−∞⌊t⌋Pqi(n)\sum_{n=-\infty}^{\lfloor t \rfloor} P_{q_i}(n)。然后我们利用 y^i\hat{y}_i 的概率密度函数，即式 (2)(2) 来推导出答案：

    ∫−∞t∑n=−∞∞Pqi(n)δ(x−n)dx=∑n=−∞∞∫−∞tPqi(n)δ(x−n)dx\begin{aligned} \int_{-\infty}^{t} \sum_{n=-\infty}^{\infty} P_{q_i}(n) \delta(x-n) dx & = \sum_{n=-\infty}^{\infty} \int_{-\infty}^{t} P_{q_i}(n) \delta(x-n) dx \end{aligned}

    根据狄拉克函数的性质，我们有

    ∫−∞tPqi(n)δ(x−n)dx={Pqi(n)n≤t∧n∈Z0others\int_{-\infty}^{t} P_{q_i}(n) \delta(x-n) dx = \begin{cases} P_{q_i}(n) & n \leq t \wedge n \in \mathbb{Z} \\ 0 & \mathrm{others} \end{cases}

    故最终可得 yiy_i 量化为区间 (−∞,t](-\infty, t] 中的任意一个整数的概率

    ∫−∞t∑n=−∞∞Pqi(n)δ(x−n)dx=∑n=−∞⌊t⌋Pqi(n)\int_{-\infty}^{t} \sum_{n=-\infty}^{\infty} P_{q_i}(n) \delta(x-n) dx = \sum_{n=-\infty}^{\lfloor t \rfloor} P_{q_i}(n)

    可以看到，结果与我们直观给出的答案一致，故可知 py^i(t)p_{\hat{y}_i}(t) 即为 y^i\hat{y}_i 的概率密度函数。

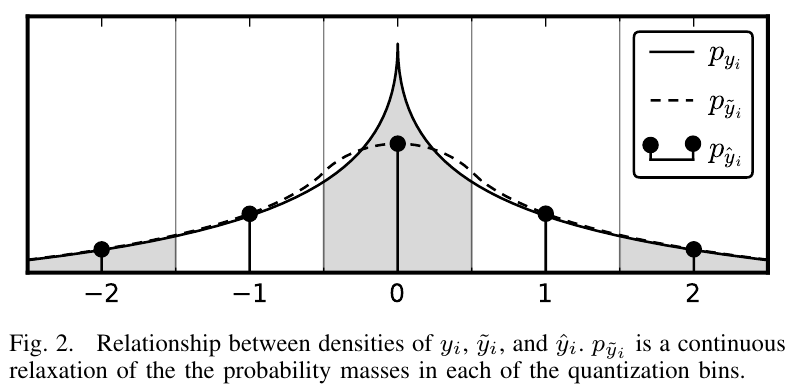
  • 结合图 Fig 2，其中 pyip_{y_i} 为 yiy_i 的概率密度函数，py^ip_{\hat{y}_i} 为 y^i\hat{y}_i 的密度函数。由于 py^ip_{\hat{y}_i} 是离散的不可微的，因此我们需要得到它的一个连续近似。

    至于为什么 pyip_{y_i} 的概率密度函数是一个拉普拉斯分布，原因在于经过一个良好的非线性变换 gag_a 后，理论上 pyip_{y_i} 基本就符合拉普拉斯分布。（待理论证明。。。）

  • 于是作者提出，如果在信号 yiy_i 上加上一个均匀噪声 Δyi\Delta y_i，且 Δyi∼rect\Delta y_i \sim \mathrm{rect}，则叠加后的信号 y~i=yi+Δyi\tilde{y}_i = y_i + \Delta y_i 满足 py~i=pyi∗rectp_{\tilde{y}_i} = p_{y_i} * \mathrm{rect}（使用概率论的知识不难证明，叠加信号的概率密度等于各分量信号的概率密度作卷积）。到此我们不难发现，py~ip_{\tilde{y}_i} 经过 py^ip_{\hat{y}_i} 的所有整数离散点，即在数轴上的整数值处，py~ip_{\tilde{y}_i} 和 py^ip_{\hat{y}_i} 相等；而在非整数值处，py^i=0p_{\hat{y}_i} = 0 但 py~ip_{\tilde{y}_i} 仍是有值且连续的，见图 Fig 2。作者通过用 y~i\tilde{y}_i 来代替 y^i\hat{y}_i，将离散不可微的标量量化近似为连续可微的标量量化。从而，原来的不可微目标函数 (1)(1) 近似为下面的可微目标函数：

    \begin{align*} L(\boldsymbol{\phi}, \boldsymbol{\theta}) & = \mathbb{E}_{\boldsymbol{x}, \boldsymbol{\Delta y}} \Big( -\log_2{p_{\boldsymbol{\tilde{y}}}(g_a(\boldsymbol{x};\boldsymbol{\phi}) + \boldsymbol{\Delta y})} \\ & \hphantom{=} + \lambda \parallel h\big(g_s(g_a(\boldsymbol{x};\boldsymbol{\phi}) + \boldsymbol{\Delta y};\boldsymbol{\theta})\big) - h(\boldsymbol{x}) \parallel \Big) \tag{3} \end{align*}

    其中，py~=∏ipy~i(y~i)p_{\boldsymbol{\tilde{y}}} = \prod_{i} p_{\tilde{y}_i} (\tilde{y}_i)。

通过对标量量化进行近似，得到可微的近似目标函数 (3)(3)，这样便可以使用 SGD 等梯度下降方法进行优化了。

4. 选择变换模型

为了展示该框架的性能，作者使用他在另一篇文章[2]中提出的模型 GDN(Generalized Divisive Normalization) 作为分析变换 gag_a，并设计一个它的逆变换作为对应的综合变换 gsg_s。此外，作者使用他二作的另一篇文章[3]中提出的 NLP(Normalized Laplacian Pyramid) 模型作为视觉感知变换 hh。

4.1 分析变换

分析变换使用 GDN 模型[2]，其构成用数学语言描述如下：

\begin{align*} \boldsymbol{y} = g_a(\boldsymbol{x};\boldsymbol{\phi}) && \text{ s.t. } &&& y_i = \frac{v_i}{(\beta_i + \sum_j \gamma_{ij} |v_j|^{\alpha_{ij}})^{\varepsilon_i}}\\ && \text{ and } &&& \boldsymbol{v} = \boldsymbol{H} \boldsymbol{x} \end{align*}

其中，参数向量 ϕ={α,β,γ,ϵ,H}\boldsymbol{\phi} = \{\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}, \boldsymbol{\epsilon}, \boldsymbol{H}\}。

4.2 综合变换

综合变换使用 GDN 模型的近似逆过程，也在文章[2]给出了，其构成用数学语言描述如下：

\begin{align*} \hat{\boldsymbol{x}} = g_s(\hat{\boldsymbol{y}};\boldsymbol{\theta}) && \text{ s.t. } &&& \hat{\boldsymbol{x}} = \boldsymbol{H}^{'} \boldsymbol{w} \\ && \text{ and } &&& w_i = \hat{y}_i \cdot (\beta_i^{'} + \sum_{j} \gamma_{ij}^{'} |\hat{y}_j|^{\alpha_{ij}^{'}})^{\varepsilon_i^{'}} \end{align*}

其中，参数向量 θ={α′,β′,γ′,ϵ′,H′}\boldsymbol{\theta} = \{\boldsymbol{\alpha}^{'}, \boldsymbol{\beta}^{'}, \boldsymbol{\gamma}^{'}, \boldsymbol{\epsilon}^{'}, \boldsymbol{H}^{'}\}。

4.3 感知变换

感知变换使用文章[3]中提出的 NLP 模型作为感知变换，在 TID2008 数据集上对 NLP 模型进行训练拟合，最后的度量效果要好于传统的客观评价指标（PSNR、SSIM 等），模型代码和实验结果见 NLPyr。

5. 实验

为了验证该框架的可行性，作者考虑了两种类型的变换，均针对 16×1616 \times 16 像素大小的图像块，一种是线性变换（θ\boldsymbol{\theta} 和 ϕ\boldsymbol{\phi} 均为只有 256×256256 \times 256 的参数），另一种是非线性变换，并用 16×1616 \times 16 的 DCT 变换（有或无死区量化）作为 Baseline。

【注】上文提到的近似离散量化器的操作只在训练阶段使用，测试阶段还是使用实际的离散量化器。

  • 数据集：训练集 ImageNet；测试集 Kodak
  • 优化器：Adam
  • Batch 大小：44
  • 输入图像大小：128×128128 \times 128

对于每一个超参 λ\lambda，分别独立训练对应的分析综合变换对。最后分别在 PSNR 和 D-NLP[3] 指标上的测试结果如下图所示：

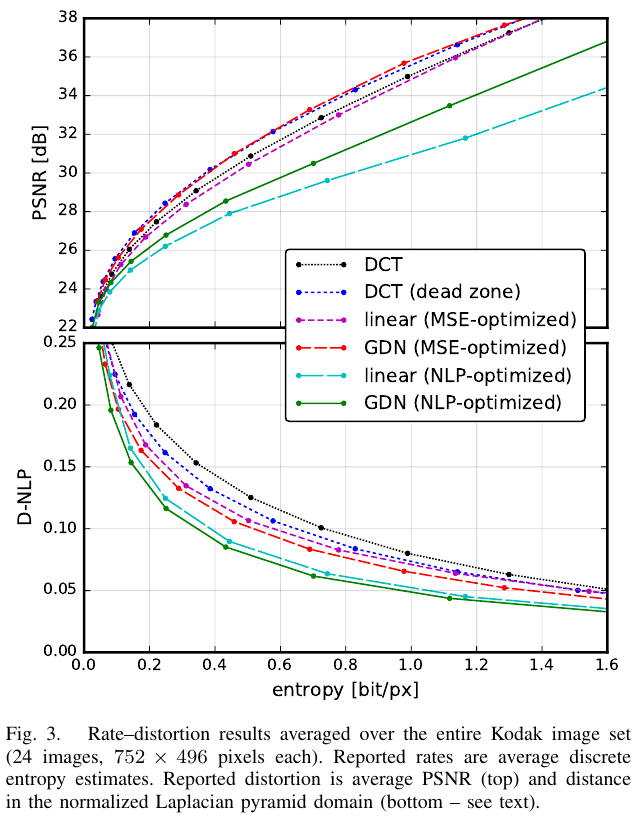
可以看到，在 PSNR 指标下，死区量化的 DCT 变换和基于 MSE 优化的 GDN 不相上下；但在 D-NLP 指标下，基于 NLP 优化的 GDN 和 Linear 都要远好于 DCT 变换。

【注】对称死区量化的性能一般要好于无死区量化的。

可视化结果参见 NLPGDN。

6. 结论

这篇文章提出一个通用的端到端优化压缩性能的框架，同时给出了近似离散量化器用于梯度下降优化的方法。通过使用 GDN 及其逆过程作为非线性变换，NLP 作为感知变换，该框架展现出了优于传统 DCT 变换的性能。

附录

  1. Ballé, J., Laparra, V., & Simoncelli, E. P. (2016, December). End-to-end optimization of nonlinear transform codes for perceptual quality. In 2016 Picture Coding Symposium (PCS) (pp. 1-5). IEEE. ↩
  2. Ballé, J., Laparra, V., & Simoncelli, E. P. (2015). Density modeling of images using a generalized normalization transformation. arXiv preprint arXiv:1511.06281. ↩
  3. Laparra, V., Ballé, J., Berardino, A., & Simoncelli, E. P. (2016). Perceptual image quality assessment using a normalized Laplacian pyramid. Electronic Imaging, 2016(16), 1-6. ↩