2017-CVPR-PointNet：Deep Learning on Point Sets for 3D Classification and Segmentation

1. 摘要

这篇文章[1]主要提出了一种用于点云数据的神经网络模型，即 PointNet。点云在 3D 视觉中是一种重要的数据结构，其主要分为几何数据和属性数据。几何数据就是每个点的 x,y,zx,y,z 坐标，而属性数据则是每个点的颜色等信息。这篇文章主要针对几何数据进行处理。由于 3D 点云这种不规则的数据格式，之前大多数深度学习方法都是将点云几何数据变换成规则的体素网格或者一系列 2D 图像的集合，但是这些方法的复杂度都太高，增加了很多不必要的计算。在这篇文章中，作者提出了一种新的用于处理点云几何数据的神经网络，它直接在点云数据上进行处理，并且很好地考虑了输入点的排列不变性。本文提出的 PointNet 模型，是一个统一的架构，可以用于各种点云任务，比如物体分类、语义分割等。虽然 PointNet 结构比较简单，但却是非常高效且有用的。从实验上来看，PointNet 展现出相当或超越 SOTA 的性能；从理论分析上来看，作者给出了 PointNet 的设计理念以及解释了 PointNet 为什么对扰动和噪声是鲁棒的。

2. 引言

传统的 CNN 架构都要求输入数据的格式是非常规则的，比如图像网络或者 3D 体素，从而实现权重共享和其他的核优化。由于点云数据是不规则的，因此以前的研究都是将点云数据转为规则的体素网格或者一系列 2D 图像的集合，然后输入网络进行处理。但这种方法会增加很多不必要的数据和计算。

针对这个原因，作者提出了直接使用点云数据的 PointNet。PointNet 是一个简单统一的点云处理模型，既避免了数据不规则也避免了转换成体素网格导致计算量大的问题，更容易进行学习。然而，PointNet 也必须考虑一个事实，即点云只是一系列点的集合，对于置换是不变的，因此在网络计算中需要一定的对称性。更进一步，关于刚体运动的不变性也需要被考虑到。

PointNet 直接接收点云数据作为输入，输出类别标签（分类）或者每个点的分割标签（分割）。PointNet 结构非常简单，每个点云数据在早期都是进行相同且独立的操作。在基础的设置下，点云的每个点都是表示为 (x,y,z)(x,y,z) 坐标；如果想要处理其它特征，则可以再增加其它的维度。

为了验证 PointNet 的有效性，作者提供了理论分析和实验评估。作者发现，PointNet 可以近似任一连续的集合函数。更有趣的现象是，PointNet 展现出可以学习到如何将输入点云总结为少数重要点的集合的能力，而这便对应了物体的粗糙轮廓。理论分析则给出了 PointNet 如此鲁棒的原因。在一系列的任务上，PointNet 不仅在性能上取得了 SOTA，而且推断速度也更快。这篇文章的主要贡献点有如下几点：

  • 设计了一个新的深度神经网络来处理无序的 3D 点云数据；
  • 展示了如何训练 PointNet 来处理分类、分割等不同任务；
  • 对 PointNet 的稳定性和有效性提供了全面的分析（即理论和实验都有）；
  • 对 PointNet 中一些选定的层给出了可视化的图解，并对其性能给出了直观解释。

使用神经网络对无序的数据集合进行处理是一个广泛且基础的问题，作者希望他们提出的方法也能够很好地迁移到其他领域。

3. 点云上的深度学习

3.1 点云属性

点云数据有以下三个主要特点：

  • 无序性：因此处理点集的神经网络应当对数据顺序不敏感；
  • 点间交互：点云数据由欧拉空间中的坐标点组成，每个点不是各自孤立的，而是相互之间有关联的；
  • 变换不变性：对于空间中的几何物体，模型在点云数据上学习到的表示应当具有一定的变换不变性。比如针对点的旋转、平移等变换，学习到的表示应当不发生变化。

3.2 模型

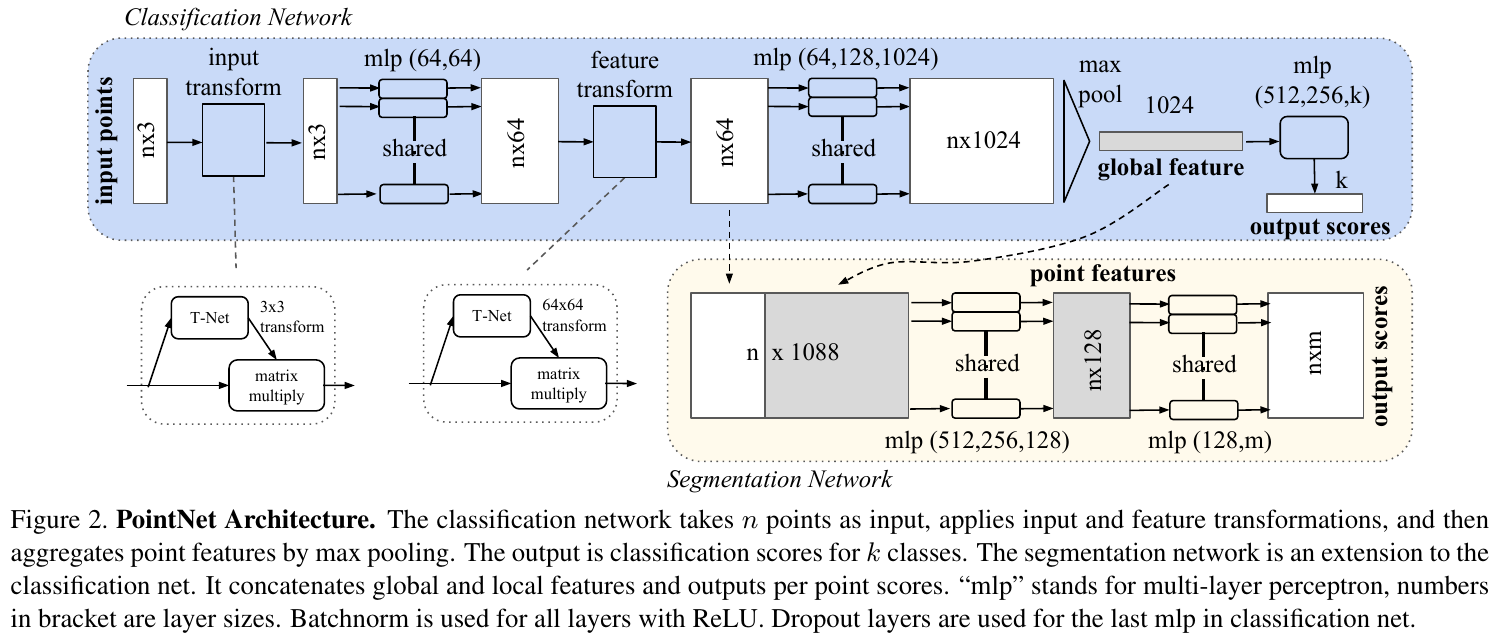
PointNet 有三个重要的模块：

  • Max Pooling：关于无序数据的对称函数；
  • Local and Global Information Combination：聚合局部信息和全局信息；
  • Joint Alignment Network：对齐输入点和点特征。

3.2.1 关于无序数据的对称函数

前面已经提到点云数据的特点，因此设计的神经网络需要对数据的顺序不敏感，一般有这几种方式：

  • 按照某种规范对无序数据进行排序；
  • 将数据当作有序的序列数据输入 RNN，但考虑数据顺序的所有组合；
  • 使用一个简单的对称函数来聚合信息，比如 ++ 和 ∗* 操作就是对称的。

然而，第一种方式只对 11 维数据有效，对更高维度的数据，无法给出一个有效的偏序关系来进行稳定排序；第二种方式虽然考虑了所有可能的顺序组合，但仍无法完全消除顺序的影响[2]，而且当数据量过大时，所有顺序组合将大到不可接受的。

因此作者考虑第三种方法，使用简单的 Max Pooling 操作作为对称函数。

3.2.2 局部和全局信息聚合

对于分割任务，除了要考虑全局信息，还要考虑局部信息的影响。因此，作者在分割网络中将局部信息和全局信息进行了聚合。具体做法就是，将 Max Pooling 得到的 10241024 维全局特征，拼接到每一个 6464 维的局部特征上，从而最终得到聚合特征 n×1088n \times 1088。

3.2.3 双对齐网络

对于语义分割任务，要求预测的标签对一定的几何变换是不变的，比如刚体变换。一种直接的方式是在对数据进行处理前先将其按照一定的规范进行对齐，比如对齐到一个规范的 x−y−zx-y-z 坐标系中。而实现这种对齐的方式可以通过对数据进行变换得到，作者就提出增加一个网络分支 T-Net，专门用来预测得到这个变换矩阵，然后将这个变换矩阵和输入的点云数据或者中间的特征数据进行矩阵相乘，实现对齐。双对齐网络即对应于 PointNet 模型中的 Input Transform 和 Feature Transform。

对于特征的对齐，其存在的一个问题是，其维度过高，因此实际优化起来比较困难。为此，作者提出可以对特征的对齐矩阵进行限制，即强制其为正交矩阵：

Lreg=∥I−AAT∥F2L_{r e g}=\left\|I-A A^{T}\right\|_{F}^{2}

3.2.4 理论分析

令 X={S:S⊆[0,1]m,∣S∣=n}\mathcal{X} = \{S: S \subseteq [0, 1]^m, |S| = n\}，f:X→Rf: \mathcal{X} \rightarrow \mathbb{R} 是一个在 X\mathcal{X} 的关于 Hausdorff 距离 dH(⋅,⋅)d_H(\cdot, \cdot) 的连续函数。

ff 为关于 dH(⋅,⋅)d_H(\cdot,\cdot) 的连续函数，即 ∀ε>0,∃δ>0\forall \varepsilon > 0, \exist \delta > 0，对任意的 S,S′∈XS, S^{'} \in \mathcal{X}，如果 dH(S,S′)<δd_H(S, S^{'}) < \delta，则有 ∣f(S)−f(S′)<ε|f(S) - f(S^{'}) < \varepsilon。

  • 定理一：∀ε>0\forall \varepsilon > 0，存在一个连线函数 hh 和对称函数 g(x1,⋯ ,xn)=γ⊙max⁡g(x_1, \cdots, x_n) = \gamma \odot \max，使得对任意的 S∈XS \in \mathcal{X}，有

    ∣f(S)−γ(max⁡xi∈S{h(xi)})∣<ε\left\lvert f(S) - \gamma\left(\max_{x_i \in S}\{h(x_i)\}\right)\right\rvert < \varepsilon

    其中，x1,⋯ ,xnx_1, \cdots, x_n 是 SS 中的所有元素的一个随意顺序组合，γ\gamma 是一个连续函数，max⁡\max 为向量 element-wise 取最大值操作，其对向量的每一维度取最大值。

    这个定理主要说明的是，PointNet 可以拟合任意的点云集合。

  • 定理二：假设 u:X→RK\boldsymbol{u}: \mathcal{X} \rightarrow \mathbb{R}^K 使得 u=max⁡xi∈S{h(xi)}\boldsymbol{u} = \max_{x_i \in S}\{h(x_i)\} 且 f=γ⊙uf = \gamma \odot \boldsymbol{u}，则有

    \begin{align*} &(a)\quad \forall S, \exist \mathcal{C}_S, \mathcal{N}_s \subseteq \mathcal{X}, f(T) = f(S)\quad \text{ if } \mathcal{C}_S \subseteq T \subseteq \mathcal{N}_S \\ &(b)\quad \lvert \mathcal{C}_S \rvert \leq K \end{align*}

    这个定理主要说明的是，即使对 PointNet 增加一些输入扰动点，也不会影响其最终的结果。

对于这两个定理的证明，原论文在补充材料中给出了，但本人看的一头雾水（感觉好多地方有问题）……（如有看懂的小伙伴，还望不吝赐教～

4. 实验

4.1 3D 任务

作者为了验证 PointNet 的有效性，在 3D 物体分类、物体分割和语义分割任务上进行了实验。

  • 3D 物体分类：作者在 ModelNet40 数据集上进行了实验，基本达到了 SOTA 的效果：

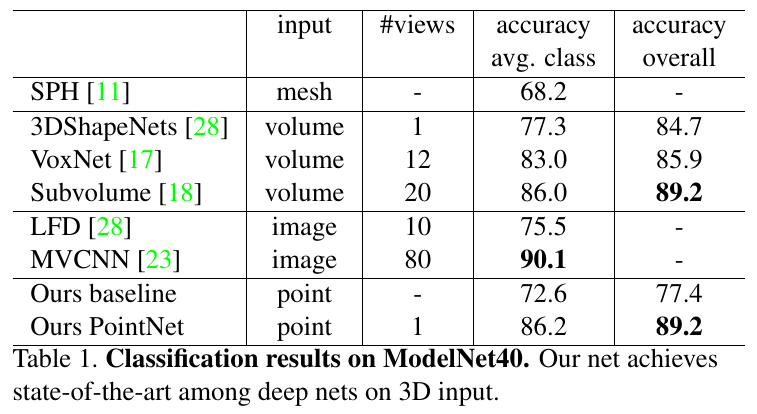
  • 3D 物体分割： 作者在部分 ShapeNet 数据集上进行了实验，结果如下：

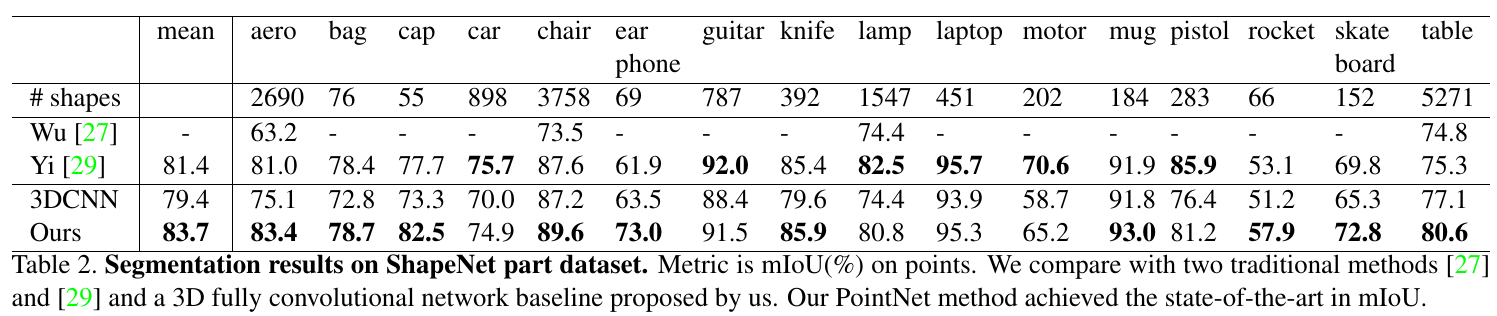
  • 3D 语义分割：作者在 Stanford 3D semantic 数据集 上进行了实验，结果如下：

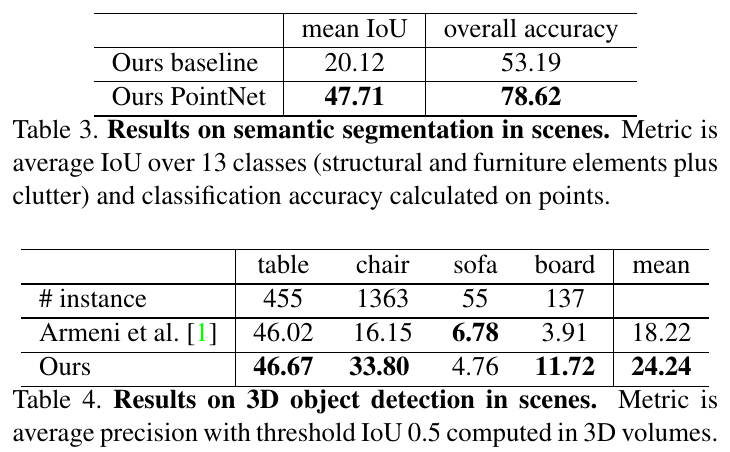
    其中，baseline 是使用手工设计特征的实验结果。

4.2 架构设计分析

作者以消融实验的方式，分析了 PointNet 网络如此设计的理由。

  • MLP + Max Pooling：作者分别对比了不使用对称函数的三种处理点云数据的方式，即 MLP(unsorted input)、MLP(sorted input) 和 LSTM，以及使用 MLP + 三种不同的对称函数的方式。结果如下图所示，MLP + Max pooling 的方法性能最好：

​

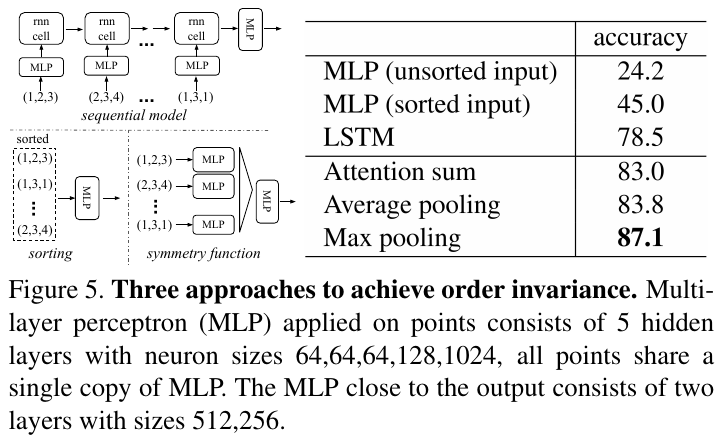
  • Input Feature Transforms：作者对比了使用 Input Transform 和 Feature Transform，以及对 Feature Transform 加上正则项损失的性能，最后发现综合使用 Input Transform + Feature Transform + Reg Loss 性能最好：

  • 鲁棒性测试：作者最后 PointNet 网络的鲁棒性能，分别使用了三种方式：丢弃部分点、增加异常点、对点加高斯噪声扰动。

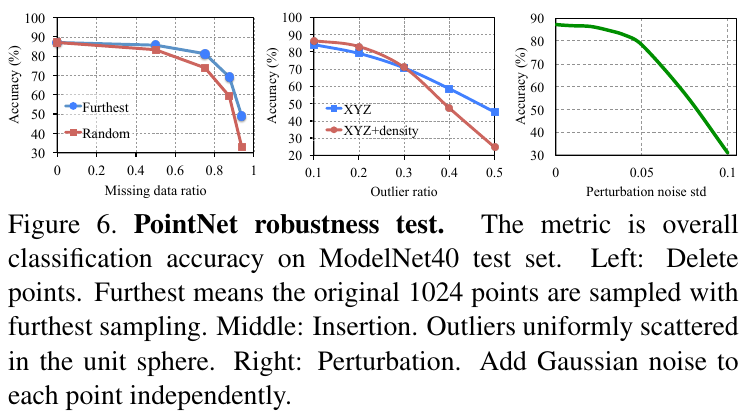
4.3 可视化

作者对定理二给出了可视化展示，如下图所示：

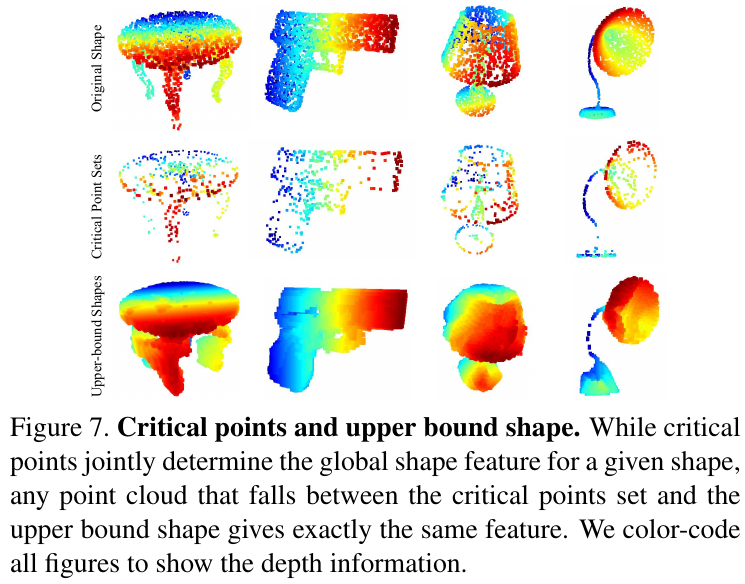
4.4 复杂度分析

作者和其它 3D 神经网络模型进行了复杂度对比， 如下图所示：

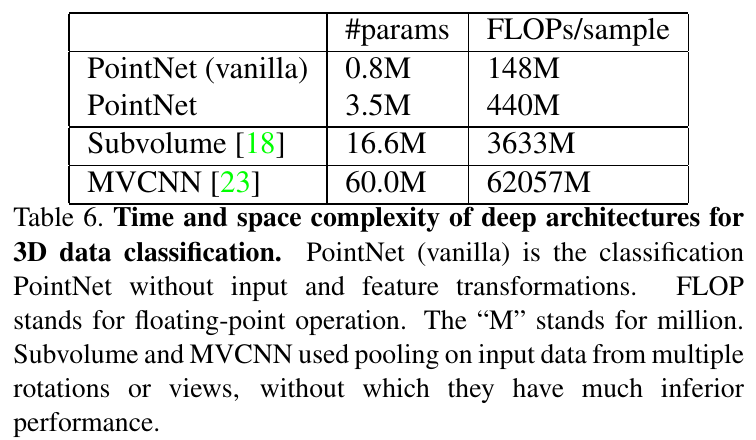
5. 结论

作者提出了一种能够直接处理点云数据神经网络 PointNet，其在 3D High Level 任务上都取得不错的结果。同时，作者对 PointNet 的设计给出了理论和实验上的分析。

附录

  1. Qi, C. R., Su, H., Mo, K., & Guibas, L. J. (2017). Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 652-660). ↩
  2. Vinyals, O., Bengio, S., & Kudlur, M. (2015). Order matters: Sequence to sequence for sets. arXiv preprint arXiv:1511.06391. ↩