2018-ICLR-Variational image compression with a scale Hyper-prior

1. 摘要

这篇文章[1]在上一篇文章[2]基础上增加了一个超先验模块，用来有效地捕获隐变量空间的空间依赖信息。这个超先验可以看作是边信息，使用边信息作为先验来辅助压缩在很多标准的图像压缩算法中都广泛使用，但在基于神经网络的压缩算法中还没有得到研究。因此，作者提出了一个超先验模块，和用于压缩的 AutoEncoder 进行联合训练。作者在文章中展示了其提出方法达到了 SOTA 的性能，同时还对比了使用不同的失真度量进行训练对性能的影响。

2. 引言

最近基于深度学习的有损压缩算法在机器学习领域和图像处理领域得到了广泛重视，出现一系列的相关研究工作。这些工作的基本框架和标准的压缩算法类似，即编码时先将图像由像素域变换到隐表示域，然后在隐表示域上进行量化，再使用无损的熵编码进行压缩；解码则是逆过程。

但是在之前的方法中，用来压缩隐表示的熵模型都是将隐表示看作是完成分解开的，即其每个元素看作是各自独立的。在训练时，这些方法都是使用香农交叉熵作为码率损失：

R=Ey^∼m[−log⁡2py^(y^)](1)R=\mathbb{E}_{\hat{\boldsymbol{y}} \sim m}\left[-\log _{2} p_{\hat{\boldsymbol{y}}}(\hat{\boldsymbol{y}})\right] \tag{1}

熵最小当且仅当熵模型分布 py^(y^)p_{\hat{\boldsymbol{y}}}(\hat{\boldsymbol{y}}) 和隐表示分布 m(y^)m(\hat{\boldsymbol{y}}) 完全相同。因此如果将隐表示中元素看作是完成分解开的，则忽略了它们之间可能存在的统计关系，从而导致次优的压缩性能。

传统压缩方法用来增加压缩性能的一个有效手段是：使用额外的比特存储边信息，然后将其从 Encoder 传输到 Decoder，来辅助解码。传统的压缩方法也是将隐表示看作是分块分解的，比如 JPEG 使用固定的分块分解方法，将图像频域信息按 8×8=648 \times 8 = 64 划分成块，每个块看作是各自独立的；而 HEVC 等则是使用可变的分块分解方法，这样可以达到更高效地压缩。这种分块分解的方法便是一种边信息，特别是 HEVC 这种自适应的可变分块分解方法。

于是，作者基于此想到可以在原来的 AutoEncoder[2] 上增加一个超先验模块，用来提取隐表示的边信息。此时，整个压缩模型在一定程度上就等价于 VAE 模型了。

3. 变分模型

基于 AutoEncoder 的压缩模型[2]的优化问题用变分推断数学化描述如下：

Ex∼pxDKL[q∥py~∣x]=Ex∼pxEy~∼q[log⁡q(y~∣x)⏟=0−log⁡px∣y~(x∣y~)⏟weighted distortion −log⁡py~(y~)⏟rate ]+ const. (2)\mathbb{E}_{\boldsymbol{x} \sim p_{\boldsymbol{x}}} D_{\mathrm{KL}}\left[q \| p_{\tilde{\boldsymbol{y}} \mid \boldsymbol{x}}\right] = \mathbb{E}_{\boldsymbol{x} \sim p_{\boldsymbol{x}}} \mathbb{E}_{\tilde{\boldsymbol{y}} \sim q}[\underbrace{\cancel{\log q(\tilde{\boldsymbol{y}} \mid \boldsymbol{x})}}_{= 0} \underbrace{-\log p_{\boldsymbol{x} \mid \tilde{\boldsymbol{y}}}(\boldsymbol{x} \mid \tilde{\boldsymbol{y}})}_{\text {weighted distortion }} \underbrace{-\log p_{\tilde{\boldsymbol{y}}}(\tilde{\boldsymbol{y}})}_{\text {rate }}]+\text { const. } \tag{2}

最小化式 (2)(2) 中的 KL 散度就是优化模型的率失真性能。其中第一项展开等于 00，第二三项则分别是加权失真项和比特率项。类似于文章[2]中所分析的那样，作者对量化后的数据使用无参数的全分解概率密度模型：

py~∣ψ(y~∣ψ)=∏i(pyi∣ψ(i)(ψ(i))∗U(−12,12))(y~i)(3)p_{\tilde{\boldsymbol{y}} \mid \psi}(\tilde{\boldsymbol{y}} \mid \boldsymbol{\psi})=\prod_{i}\left(p_{y_{i} \mid \boldsymbol{\psi}^{(i)}}\left(\boldsymbol{\psi}^{(i)}\right) * \mathcal{U}\left(-\frac{1}{2}, \frac{1}{2}\right)\right)\left(\tilde{y}_{i}\right) \tag{3}

作者称该模型为 factorized-prior model。其隐表示 y\boldsymbol{y} 的可视化分析如下图所示：

可以看到，通过将隐表示的数据 y\boldsymbol{y} 中的元素分别减去其对应的均值，再除以标准差，则可以有效消除空间依赖。

4. 超先验引入

为了消除 factorized-prior model 模型隐表示的空间依赖性，于是作者引入超先验变量 z~\tilde{\boldsymbol{z}} 来捕捉隐变量的空间依赖，如下图所示：

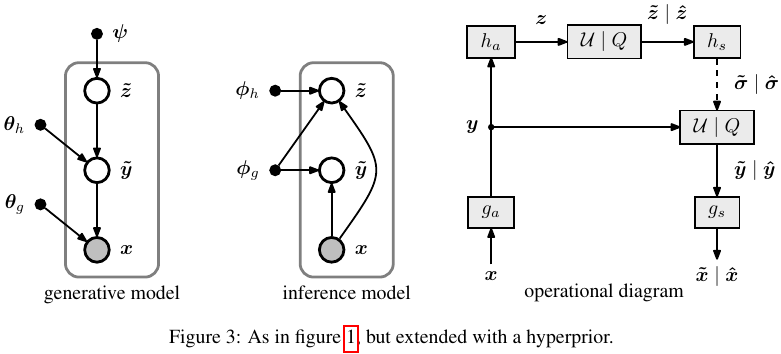
现在每一个元素 y~i\tilde{y}_i 都被建模成一个 00 均值，σi\sigma_i 标准差的高期分布，于是生成模型被扩展为：

\begin{align*} p_{\tilde{\boldsymbol{y}} \mid \tilde{\boldsymbol{z}}}\left(\tilde{\boldsymbol{y}} \mid \tilde{\boldsymbol{z}}, \boldsymbol{\theta}_{h}\right)=& \prod_{i}\left(\mathcal{N}\left(0, \tilde{\sigma}_{i}^{2}\right) * \mathcal{U}\left(-\frac{1}{2}, \frac{1}{2}\right)\right)\left(\tilde{y}_{i}\right) \\ & \text { with } \tilde{\boldsymbol{\sigma}}=h_{s}\left(\tilde{\boldsymbol{z}} ; \boldsymbol{\theta}_{h}\right) \tag{4} \end{align*}

推断模型被扩展为：

\begin{align*} q\left(\tilde{\boldsymbol{y}}, \tilde{\boldsymbol{z}} \mid \boldsymbol{x}, \boldsymbol{\phi}_{g}, \boldsymbol{\phi}_{h}\right)=& \prod_{i} \mathcal{U}\left(\tilde{y}_{i} \mid y_{i}-\frac{1}{2}, y_{i}+\frac{1}{2}\right) \cdot \prod_{j} \mathcal{U}\left(\tilde{z}_{j} \mid z_{j}-\frac{1}{2}, z_{j}+\frac{1}{2}\right) \\ & \text { with } \boldsymbol{y}=g_{a}\left(\boldsymbol{x} ; \boldsymbol{\phi}_{g}\right), \boldsymbol{z}=h_{a}\left(\boldsymbol{y} ; \boldsymbol{\phi}_{h}\right) \end{align*} \tag{5}

而超先验变量 z~\tilde{\boldsymbol{z}} 则使用非参数的全分解密度模型来建模（在 factorized-prior model 中则是对 y\boldsymbol{y}）：

pz~∣ψ(z~∣ψ)=∏i(pzi∣ψ(i)(ψ(i))∗U(−12,12))(z~i)(6)p_{\tilde{\boldsymbol{z}} \mid \psi}(\tilde{\boldsymbol{z}} \mid \boldsymbol{\psi})=\prod_{i}\left(p_{z_{i} \mid \psi^{(i)}}\left(\boldsymbol{\psi}^{(i)}\right) * \mathcal{U}\left(-\frac{1}{2}, \frac{1}{2}\right)\right)\left(\tilde{z}_{i}\right) \tag{6}

于是损失函数最终写为：

\begin{align*} \mathbb{E}_{\boldsymbol{x} \sim p_{\boldsymbol{x}}} D_{\mathrm{KL}}\left[q \| p_{\tilde{\boldsymbol{y}}, \tilde{\boldsymbol{z}} \mid \boldsymbol{x}}\right] =&\ \mathbb{E}_{\boldsymbol{x} \sim p_{\boldsymbol{x}}} \mathbb{E}_{\tilde{\boldsymbol{y}}, \tilde{\boldsymbol{z}} \sim q}[\underbrace{\cancel{\log q(\tilde{\boldsymbol{y}}, \tilde{\boldsymbol{z}} \mid \boldsymbol{x})}}_{= 0} - \log p_{\boldsymbol{x} \mid \tilde{\boldsymbol{y}}}(\boldsymbol{x} \mid \tilde{\boldsymbol{y}}) \\ &-\log p_{\tilde{\boldsymbol{y}} \mid \tilde{\boldsymbol{z}}}(\tilde{\boldsymbol{y}} \mid \tilde{\boldsymbol{z}})-\log p_{\tilde{\boldsymbol{z}}}(\tilde{\boldsymbol{z}})]+\text { const. } \tag{7} \end{align*}

其中第一项展开为 00，第二三四项分别为失真项、y~\tilde{\boldsymbol{y}} 的码率项和 z~\tilde{\boldsymbol{z}} 的码率项（也可称为边信息项）。

5. 模型

作者最终给出的模型架构如下：

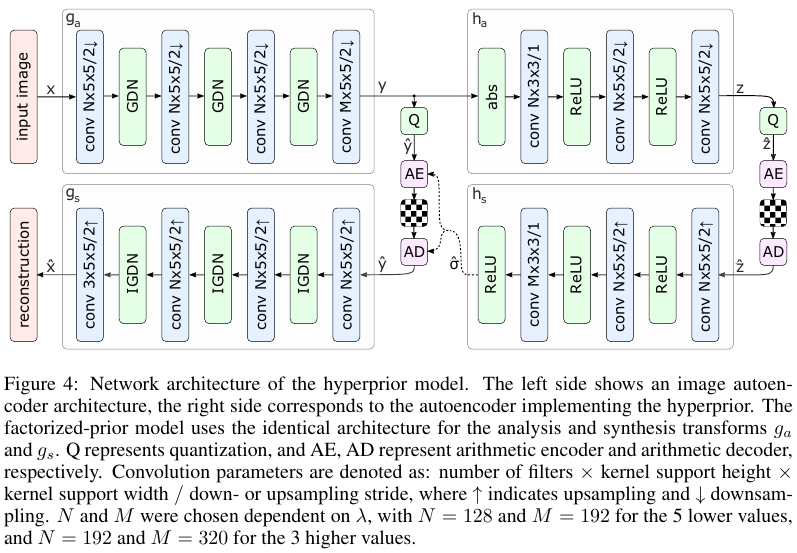
6. 实验

作者用网上爬取的图像作为训练集，在 Kodak 上进行测试，性能如下：

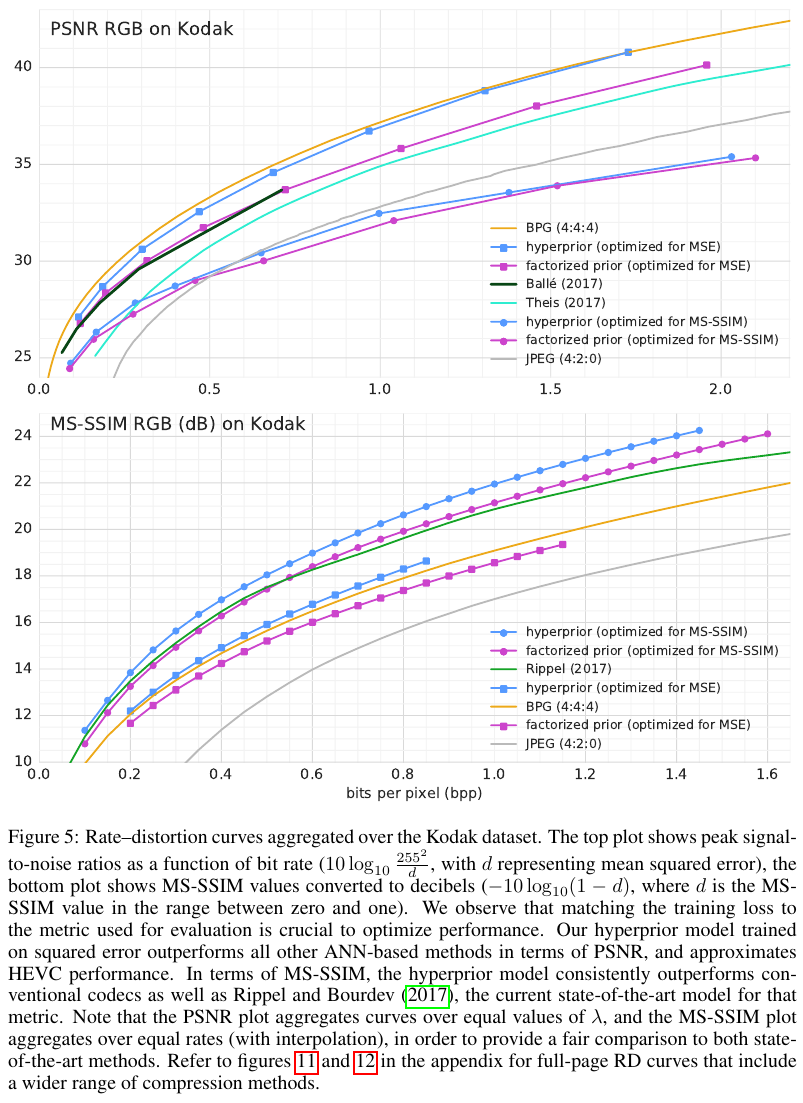
此外，作者还对比了边信息大小和图像 bpp 大小的关系，如下图：

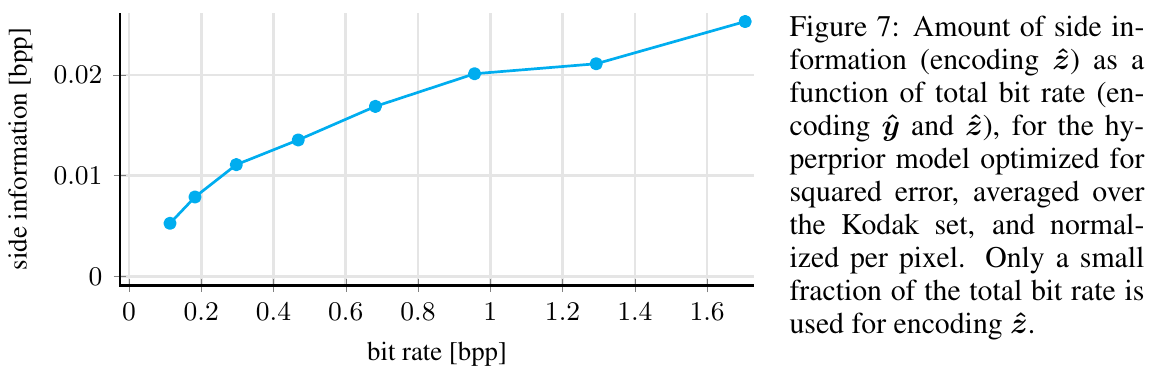
7. 总结

引入超先验模型，类似于传统方法中的边信息，能有效辅助 AutoEncoder 压缩模型提高压缩性能。

附录

  1. Ballé, J., Minnen, D., Singh, S., Hwang, S. J., & Johnston, N. (2018, February). Variational image compression with a scale hyperprior. In International Conference on Learning Representations. ↩
  2. Ballé, J., Laparra, V., & Simoncelli, E. P. (2017). End-to-end optimized image compression. In 5th International Conference on Learning Representations, ICLR 2017. ↩