【注】学习笔记参考自《统计学习方法第二版》——李航。

1. 简介

对于一般的统计模型来说，下图描述了训练误差和测试误差与模型的复杂度之间的关系：

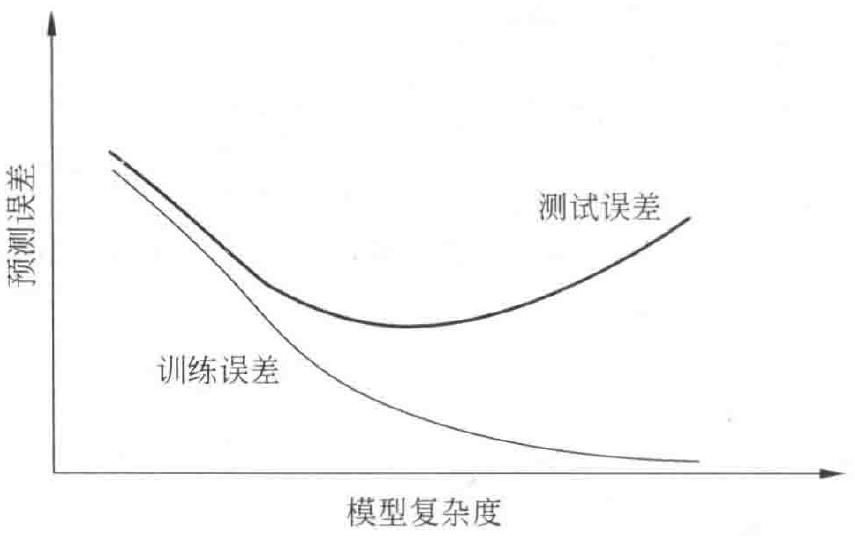
当模型的复杂度增大时，训练误差会逐渐减小并趋向于 $0$，而测试误差会先减小，达到最小值后增大；当选择的模型复杂度过大时，过拟合现象就会出现。因此，在学习时就要防止过拟合，进行最优的模型选择，即选择复杂度适当的模型，以达到使测试误差最小的学习目的。常用的两种模型选择方法：正则化与交叉验证。

2. 正则化

正则化是结构风险最小化策略的实现，是在经验风险上加上一个正则化项或惩罚项。正则化项一般时模型复杂度的单调递增函数，模型越复杂，正则化值就越大。

• 正则化一般就有如下形式：

$$\begin{array}{c} \mathrm{min}_{f \in \mathcal{F}} \frac{1}{N} \sum_{i=1}^N L(y_i,f(x_i)) + \lambda J(f) \end{array}$$

其中，第一项是经验风险，第二项时正则化项，$\lambda \geq 0$ 为调整二者之间关系的系数。

正则化项可以取不同的形式，比如在回归问题中，正则化项可以取 $L_1$ 范数：

$$\begin{array}{c} L(w) = \frac{1}{N} \sum_{i=1}^N (f(x_i;w) - y_i)^2 + \frac{\lambda}{2} \parallel w \parallel \end{array}$$

或者 $L_2$ 范数：

$$\begin{array}{c} L(w) = \frac{1}{N} \sum_{i=1}^N (f(x_i;w) - y_i)^2 + \frac{\lambda}{2} \parallel w \parallel^2 \end{array}$$

• 正则化项符合奥卡姆剃刀原理：即在所有可能选择的模型中，能够很好地解释已知数据并且十分简单才是最好的模型，也就是应用选择的模型。
• 从贝叶斯估计的角度来看，正则化项对应于模型的先验概率。可以假设为复杂模型具有较小的先验概率，简单模型具有较大的先验概率。

3. 交叉验证

交叉验证是另一种常用的模型选择方法。

• 简单交叉验证：首先随机地将已给数据分为两部分，一部分作为训练集，另一部分作为测试集（一般选择 $70\%$ 的数据作为训练集，$30\%$ 的数据作为测试集）；然后用训练集在各种条件下训练模型，从而得到不同的模型；最后在测试集上评价各个模型的测试误差，选出测试误差最小的模型。
• $S$ 折交叉验证：首先随机地将已给数据切分为 $S$ 各互不相交、大小相同的子集；然后利用 $S-1$ 个子集的数据训练模型，利用余下的子集测试模型；将这一过程对可能的 $S$ 种选择重复进行；最后选出 $S$ 次评测中平均测试误差最小的模型。
• 留一交叉验证：$S$ 折交叉验证的特殊情形是 $S = N$，称为留一交叉验证，往往在数据缺乏的情况下使用。其中 $N$ 为给定数据集的容量。