1. IEEE 754 标准

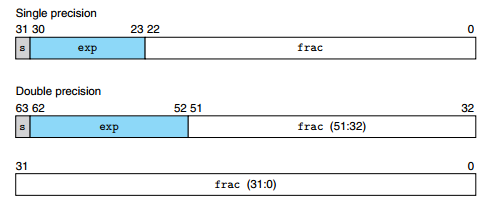
IEEE 754 浮点标准用 $V = (-1)^s \times M \times 2^E$ 的形式来表示一个数。

• 符号位（s）：指明数的正负，即 $V$ 中的 $s$。

• 阶码（exp）：对浮点数加权，即 $V$ 中的 $E$。

• 尾数（frac）：二进制小数，即 $V$ 中的 $M$，范围为 $1 \sim 2 - \varepsilon$（规格化数），或者是 $0 \sim 1 - \varepsilon$（非规格化数），其中 $\varepsilon = 2^{-|frac|}$，$|frac|$ 为尾数所占有的位数。

2. 浮点数数值分类

• 以单精度为例：

2.1 规格化的值

阶码的位模式（二进制码）既不全为 0 也不全为 1 。

• 阶码的值 $E = e - Bias$ 。其中 $e$ 为阶码的位模式对应的无符号数；$Bias = 2^{k-1} - 1$，$k$ 为阶码的位数（单精度 $Bias = 127$、双精度 $Bias = 1023$）。

• 尾码的值 $M = 1 + f$ 。$f$ 为 $frac = f_{n-1} \cdots f_1 f_0$ 描述的小数值 $0.f_{n-1} \cdots f_1 f_0$，$n = |frac|$。即 $M = 1.f_{n-1} \cdots f_1 f_0$，在计算机里以 $frac$ 表示时去掉了总为 1 的首位（节省了一位空间）。

2.2 非规格化的值

阶码的位模式（二进制码）为全 0 。

• 阶码的值 $E = 1 - Bias$ 。$Bias = 2^{k-1} - 1$，$k$ 为阶码的位数（单精度 $Bias = 127$、双精度 $Bias = 1023$）。

• 尾码的值 $M = f$ 。$f$ 为 $frac = f_{n-1} \cdots f_1 f_0$ 描述的小数值 $0.f_{n-1} \cdots f_1 f_0$。

非规格化数的作用

1. 提供了一种表示 0 的方法

对于规格化数，由于 $M \geq 1$，故无法使用规格化数表示 0 。

• $+0.0$：符号位为 0，阶码为全 0，尾数为全 0 。
• $-0.0$：符号位为 1，阶码为全 0，尾数为全 0 。

【注】IEEE 的浮点格式中，$+0.0$ 和 $-0.0$ 在某些方面被认为是不同的，而在其他方面是相同的。

2. 表示那些接近 0 的数

非规格化数能够均匀地表示那些接近 0 的数。这种属性被称为 逐渐溢出，即非规格化数所表示的数值分布均匀地接近 0.0 。

2.3 特殊值

阶码全为 1 。

• 尾数全为 0：得到的值表示无穷。当 $s = 0$ 是为 $+\infty$；当 $s = 1$ 是为 $-\infty$ 。用于表示溢出的结果，比如两个非常大的数相乘溢出了。

• 尾数为非 0：得到的值表示不是一个数值，即 $NaN$ 。用于表示一些非法的运算结果，如 $\sqrt{-1}$ 或 $\infty - \infty$ 等，也可以用来表示未初始化的值。

2.4 举例

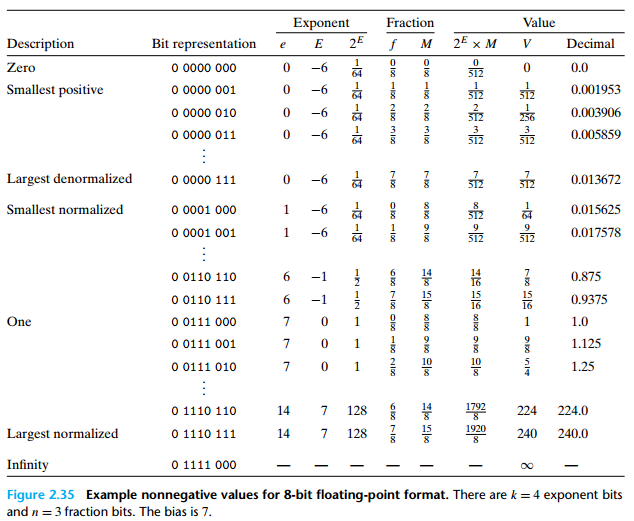
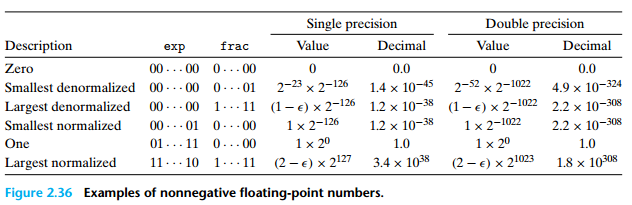
3. 浮点数数值舍入

IEEE 浮点格式定义了四种不同格式的舍入方式，默认的方法是向偶数舍入。

3.1 向上舍入

$\hat{x} = \lceil x \rceil$ 。

3.2 向下舍入

$\hat{x} = \lfloor x \rfloor$ 。

3.3 向偶数舍入

将数字向上或向下舍入，使得结果的最低有效数字是偶数。

3.4 向零舍入

• x > 0：向下舍入。
• x < 0：向上舍入。

4. 运算

4.1 浮点加法

• 满足交换律：$x +^f y = y +^f x$
• 基本满足单调性：$\forall x \ne NaN, a \geq b \iff a + x \geq b + x$
• 存在单位元：$0.0$
• 基本存在逆元：$x +^f (-x) = 0.0$
  除了 $NaN, \pm \infty$ 不满足有逆元外，其他数值都满足存在逆元。
• 不满足可结合性：由于存在精度损失，导致浮点数加法无法满足可结合性，比如：

$$\begin{array}{c} (3.14 + 10^{10}) - 10^{10} = 0.0 \\ 3.14 + (10^{10} - 10^{10}) = 3.14 \end{array}$$

4.2 浮点乘法

• 满足交换律：$x \times^f y = y \times^f x$
• 基本满足单调性：$\forall x \ne NaN, a \geq b \iff ((x \geq 0) \land (a \times^f x \geq b \times^f x)) \lor ((x \leq 0) \land (a \times^f x \leq b \times^f x))$
• 存在单位元：$1.0$
• 不满足可结合性：

$$\begin{array}{c} (10^{20} \times 10^{20}) \times 10^{-20} = +\infty \\ 10^{20} \times (10^{20} \times 10^{-20}) = 10^{20} \end{array}$$

• 对加法不满足分配律：

$$\begin{array}{c} 10^{20} \times (10^{20} - 10^{20}) = 0.0 \\ 10^{20} \times 10^{20} - 10^{20} \times 10^{20} = NaN \end{array}$$

4.3 精度

• 对于规格化数：单精度浮点数有效位数为 24 位，双精度浮点数有效位数为 53 位（隐含尾数未显示的首位 1 ）。

• 对于非规格化数：单精度浮点数有效位数为 23 位， 双精度浮点数有效位数为 52 位。

比如：对于单精度浮点运算：

$$\begin{array}{c} (1 \lt\lt 24) + 1 = (1 \lt\lt 24) \end{array}$$

因为浮点数加法首先需要将指数较小的数的指数调整到指数较大的数，然后再将尾数相加。因此这里当把 $1$ 的指数调整到 $1 \lt\lt 24$ 的指数大小时，由于尾数精度只有 $23$ 位，因此尾数精度不够导致 $1$ 最后丢失。