将传染病范围内的人群分为以下类别:
- S(Susceptible)类:指未得病,但与感染者接触后容易收到感染的人。
- E(Exposed)类:指接触过感染者,但暂时没有传播的能力的人。
- I(Infectious)类:指染上传染病,具有传播能力的人。(可以传播给S类人员,将其变成E类或I类成员)
- R(Recovered / Removed)类:指病愈而具有免疫力的人或被隔离的移出者。(如果免疫期有限,R类人员可以重新变为S类)
1. SI模型
1.1 模型假设
- 将人群分为S类和I类,在疾病传播期内所考察地区的总人数K不变(即不考虑生死和迁移)。时刻t这两类人群人数分别记为S(t)和I(t)。
- 每个传染病患者每天有效接触的平均人数为β(称为日接触率)。当传染病患者与健康人接触会将健康人感染为传染病患者。
- 初始时刻传染病患者人数为I0。
1.2 模型建立
由以上假设可建立如下的微分方程:
dtdI(t)=βI(t)KS(t)S(t)+I(t)=KI(0)=I0
1.3 模型求解
联立方程可得:
dtdI(t)=βI(t)(1−KI(t))
进一步化简可得:
dtdKI(t)=βKI(t)(1−KI(t))
令i(t)=KI(t),则i(t)称为感染率。得:
dtdi(t)=βi(t)(1−i(t))i0=i(0)=KI0
上述方程为logistic模型,其解为:
i(t)=1+e−βt(i01−1)1
i(t) ~ t和dtdi(t) ~ i(t)的图像如下: 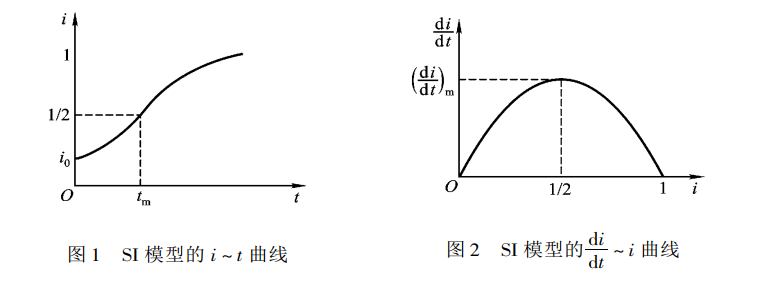
由上图可知,当i(t)=21时,dtdi(t)达到最大值(dtdi(t))m,此时
tm=β−1ln(i01−1)
2. SIS模型
1.4 模型假设
- 将人群分为S类和I类,在疾病传播期内所考察地区的总人数K不变(即不考虑生死和迁移)。时刻t这两类人群人数分别记为S(t)和I(t)。
- 每个传染病患者每天有效接触的平均人数为β(称为日接触率)。当传染病患者与健康人接触会将健康人感染为传染病患者。
- 每天被治愈的患者数占总患者的比率为常熟μ(称为日治愈率)。病人治愈后成为仍可被感染的健康人。易知μ1为传染病的平均传染期。
- 初始时刻传染病患者人数为I0。
1.5 模型建立
由以上假设可以建立如下微分方程:
dtdI(t)=βI(t)KS(t)−μI(t)S(t)+I(t)=KI(0)=I0
1.6 模型求解
联立方程可得:
dtdI(t)=βI(t)(1−KI(t))−μI(t)
进一步化简可得:
dtdKI(t)=βKI(t)(1−KI(t))−μKI(t)
令i(t)=KI(t),则i(t)称为感染率。得:
dtdi(t)=βi(t)(1−i(t))−μi(t)
令σ=μβ,可知σ是整个传染期内每个患者有效接触的平均人数,称为接触数。得:
dtdi(t)=−βi(t)(i(t)−(1−σ1))i0=i(0)=KI0
由以上方程可得SIS模型的dtdi(t) ~ i(t)和i(t) ~ t图像: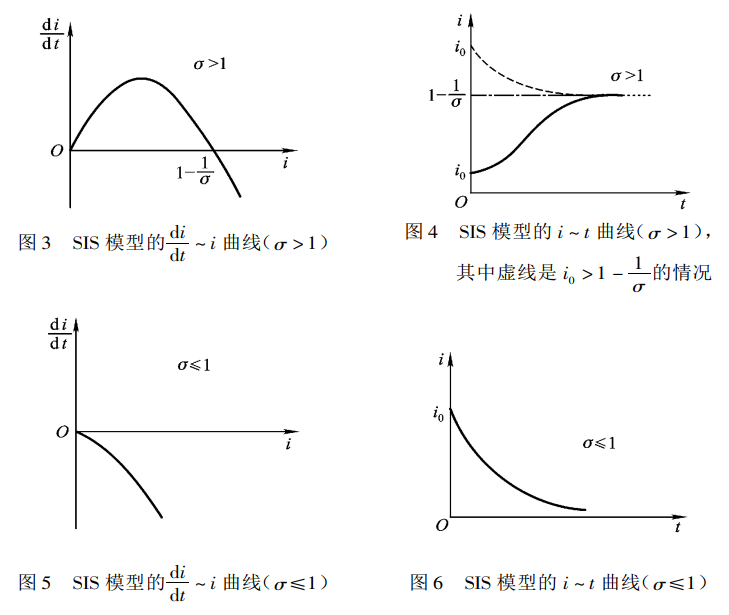
3. SIR模型
3.1 模型假设
- 将人群分为健康人(S类)、传染病患者(I类)和病愈/死亡的移出者(R类)(免疫期近似∞),在疾病传播期内所考察地区的总人数K不变。时刻t这三类人群人数分别记为S(t)、I(t)和R(t)。
- 传染病患者的日接触率为β,日治愈率为μ,传染期接触的总人数为σ=μβ。
- 初始时刻的健康人数和患者数分别为S0、I0。
3.2 模型建立
由以上假设可以建立如下微分方程:
dtdS(t)=−βI(t)KS(t)dtdI(t)=βI(t)KS(t)−μI(t)S(t)+I(t)+R(t)=KS(0)=S0I(0)=I0
令s(t)=KS(t),则s(t)称为未感染率;令i(t)=KI(t),则i(t)称为感染患病率;令r(t)=KR(t),则r(t)称为移出率。
上述方程可进一步化简为:
dtds(t)=−βi(t)s(t)dtdi(t)=βi(t)s(t)−μi(t)s(t)+i(t)+r(t)=1s0=s(0)=KS0i0=i(0)=KI0
上述方程的解析解很难解出,可以利用仿真计算帮助我们分析该模型。
3.3 模型仿真
设K=10000,β=1,μ=0.3,s0=0.98,i0=0.02。
- 利用AnyLogic仿真软件仿真模型如下:
- 仿真数据:
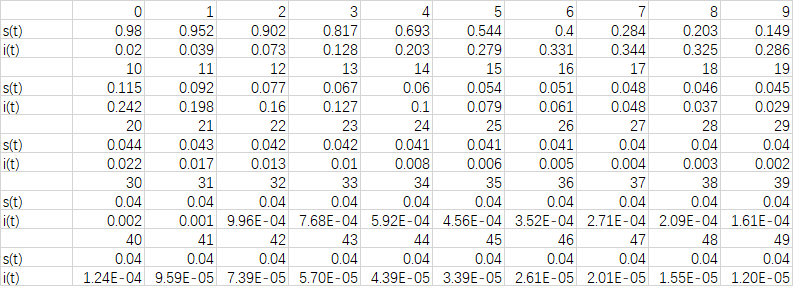
- 仿真图像:
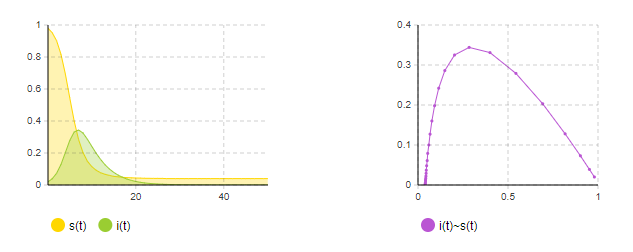
- 利用matlab仿真模型如下:
1
2
3
4
5
| function y = ill(t,x)
a = 1
b = 0.3
y = [a*x(1)*x(2) - b*x(1), -a*x(1)*x(2)]'
end
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| ts = 0:50;
x0 = [0.02, 0.98];
[t, x] = ode45
figure
plot, t, x)
title、i~t图像");
xlabel("t/天");
ylabel("s/i");
legend("i","s");
grid
figure
plot(x(:,2), x(:,1))
title("i~s图像");
xlabel("s");
ylabel("i");
grid
|
- 仿真数据:

- 仿真图像:
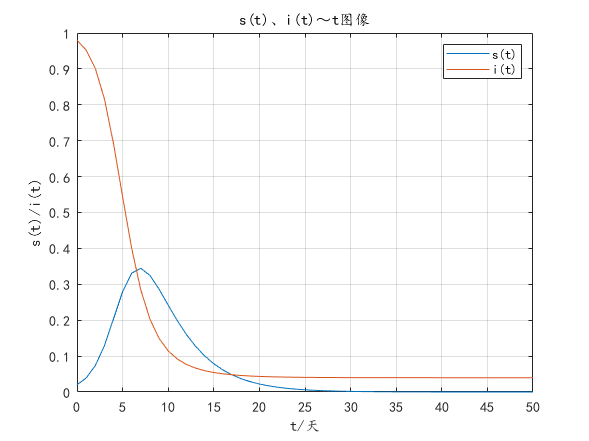 |
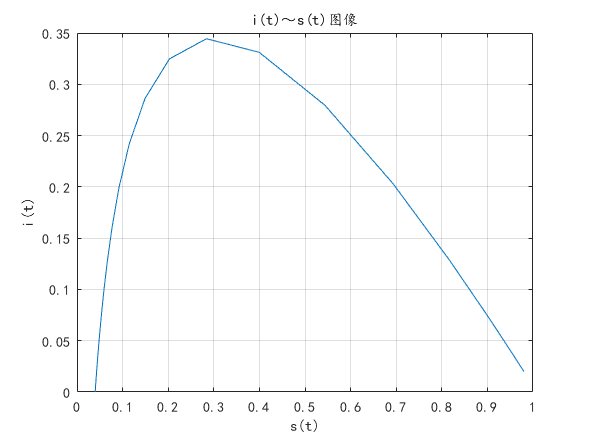 |
| s(t)、i(t)与t的图像 |
i(t)与s(t)的图像 |
3.4 模型分析
- 相轨线定义(摘自百度百科——相轨线)
对于微分方程:
dtdx=P(t,x,y)dtdy=Q(t,x,y)x(t0)=x0y(t0)=y0
其解为:
x=x(t)y=y(t)
则该组解在xOy平面(称为相平面)所描绘的曲线即相轨线。
- 相轨线分析
由以上可知,s~i平面成为相平面,相轨线在相平面上的定义域为:
D={(s,t)∣s≥0,i≥0,s+i≤1}
令 σ=μβ(含义同SIS模型)。
对SIR模型微分方程:
dtds(t)=−βi(t)s(t)dtdi(t)=βi(t)s(t)−μi(t)
相除消去dt,得:
dsdi=σs1−1i∣s=s0=i0
可求得方程的解为:
i=(s0+i0)−s+σ1lns0s
由方程可知SIR模型的相轨线:
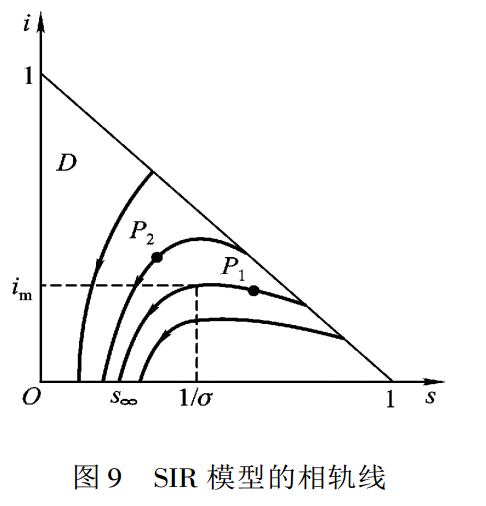
分析如上曲线可得SIR模型以下性质:
- 不论初始条件s0、i0如何,病人终将消失,即
i∞=0
- 最终未被感染的健康者的比例是s∞,s∞是方程
s0+i0−s∞+σ1lnss∞=0
在(0,σ1)内的根。
- 若s0>σ1,则i(t)先增加后减小;当s=σ1时,i(t)达到最大值
im=s0+i0−σ1
然后i(t)单调减小且趋于0,s(t)则单调减小至s∞。
- 若s0≤σ1,则i(t)单调减小至零,s(t)单调减小至s∞。
可以看出,σ1是一个阈值,当s0>σ1时传染病就会蔓延,而当s0≤σ1时传染病就不会蔓延。
在σ=μβ中,人们的卫生水平越高,日接触率β越小;医疗水平越高,日治愈率μ越大。可知,提高医疗卫生水平有助于控制传染病的蔓延。
另外,σs=βsμ1是传染期内一个病人传染的健康者的平均数,称为交换数,其含义为一个病人被σs个健康者交换。故当s0≤σ1,即σs0≤1时,必有σs≤1,即交换数不超过1,此时病人比例i(t)不会增加,传染病不会蔓延。
4. SIRS模型
4.1 模型假设
- 将人群分为健康人(S类)、传染病患者(I类)和病愈的移出者(R类)(免疫期近似∞),在疾病传播期内所考察地区的总人数K不变。时刻t这三类人群人数分别记为S(t)、I(t)和R(t)。
- 传染病患者的日接触率为β,日治愈率为μ,传染期接触的总人数为σ=μβ。
- 初始时刻的健康人数和患者数分别为S0、I0。
4.2 模型建立







