矩阵微分

独立性假设

假定实值函数的向量变元 x=[xi]i=1m∈Rm \boldsymbol{x} = [x_i]_{i=1}^m \in \mathbb{R}^m 或者矩阵变元 X=[xij]i=1,j=1m,n∈Rm×n \boldsymbol{X} = [x_{ij}]_{i=1,j=1}^{m,n} \in \mathbb{R}^{m \times n} 本身无任何特殊结构，即向量或矩阵变元的元素之间是各自独立的。用数学公式表达如下：

∂xi∂xj=δij={1i=j0others∂xkl∂xij=δkiδlj={1k=i∩l=j0others\begin{array}{c} \frac{\partial x_i}{\partial x_j} = \delta_{ij} = \begin{cases} 1 & i = j \\ 0 & others \end{cases} \\ \frac{\partial x_{kl}}{\partial x_{ij}} = \delta_{ki} \delta_{lj} = \begin{cases} 1 & k = i \cap l = j \\ 0 & others \end{cases} \end{array}

1. 符号定义及实值函数分类

2. 定义

2.1 矩阵的向量化

  • 列向量化：矩阵 A∈Rm×n\boldsymbol{A} \in \mathbb{R}^{m \times n} 的向量化 vec(A)\mathrm{vec}(\boldsymbol{A}) 是一个线性变换，它将矩阵 A=[aij] \boldsymbol{A} = [a_{ij}] 的元素按列堆栈，排列成一个 mn×1mn \times 1 的向量，即

vec(A)=[a11,⋯ ,am1,⋯ ,a1n,⋯ ,amn]T\begin{array}{c} \mathrm{vec}(\boldsymbol{A}) = [a_{11}, \cdots, a_{m1}, \cdots, a_{1n}, \cdots, a_{mn}]^T \end{array}

  • 行向量化：类似地，矩阵 A\boldsymbol{A} 的行向量化为

rvec(A)=[a11,⋯ ,a1n,⋯ ,am1,⋯ ,amn]\begin{array}{c} \mathrm{rvec}(\boldsymbol{A}) = [a_{11}, \cdots, a_{1n}, \cdots, a_{m1}, \cdots, a_{mn}] \end{array}

2.2 向量的矩阵化

一个 mn×1mn \times 1 向量 a=[a1,⋯ ,amn]T \boldsymbol{a} = [a_1, \cdots, a_{mn}]^T 转换为一个 m×nm \times n 矩阵 A\boldsymbol{A} 的运算称为矩阵化，用符号 unvecm,n(a)\mathrm{unvec}_{m,n}(\boldsymbol{a}) 表示，定义为

Am×n=unvecm,n(a)=[a1am+1⋯am(n−1)+1a2am+2⋯am(n−1)+2⋮⋮⋱⋮ama2m⋯amn]\begin{array}{c} \boldsymbol{A}_{m \times n} = \mathrm{unvec}_{m, n}(\boldsymbol{a}) = \left[ \begin{matrix} a_1 & a_{m+1} & \cdots & a_{m(n-1)+1} \\ a_2 & a_{m+2} & \cdots & a_{m(n-1)+2} \\ \vdots & \vdots & \ddots & \vdots \\ a_m & a_{2m} & \cdots & a_{mn} \end{matrix} \right] \end{array}

2.3 偏导算子

  • 1×m1 \times m 行向量偏导算子记为：

Dx=def∂∂xT=[∂∂x1,⋯ ,∂∂xm]\begin{array}{c} D_{\boldsymbol{x}} \overset{\mathrm{def}}{=} \frac{\partial}{\partial \boldsymbol{x}^T} = [ \frac{\partial}{\partial x_1}, \cdots, \frac{\partial}{\partial x_m} ] \end{array}

  • n×mn \times m 矩阵偏导算子存在两种可能的定义，分别记为：

DX=[∂∂x11⋯∂∂xm1⋮⋱⋮∂∂x1n⋯∂∂xmn]\begin{array}{c} D_{\boldsymbol{X}} = \left[ \begin{matrix} \frac{\partial}{\partial x_{11}} & \cdots & \frac{\partial}{\partial x_{m1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial}{\partial x_{1n}} & \cdots & \frac{\partial}{\partial x_{mn}} \end{matrix} \right] \end{array}

和

DrvecX=[∂∂x11,⋯ ,∂∂xm1,⋯ ,∂∂x1n,⋯ ,∂∂xmn]\begin{array}{c} D_{\mathrm{rvec} \boldsymbol{X}} = [\frac{\partial}{\partial x_{11}}, \cdots, \frac{\partial}{\partial x_{m1}}, \cdots, \frac{\partial}{\partial x_{1n}}, \cdots, \frac{\partial}{\partial x_{mn}}] \end{array}

前者称为矩阵变元 X\boldsymbol{X} 的 Jacobian 矩阵算子，后者称为矩阵变元 X\boldsymbol{X} 列向量化（vec\mathrm{vec}）后的行偏导向量算子。此二者关系为：

DrvecX=rvec(DX)=(vec(DXT))T\begin{array}{c} D_{\mathrm{rvec}\boldsymbol{X}} = \mathrm{rvec}(D_{\boldsymbol{X}}) = (\mathrm{vec}(D_{\boldsymbol{X}}^T))^T \end{array}

  • m×1m \times 1 列向量偏导算子（习惯称为梯度算子）记为：

∇x=def∂∂x=[∂∂x1,⋯ ,∂∂xm]T\begin{array}{c} \nabla_{\boldsymbol{x}} \overset{\mathrm{def}}{=} \frac{\partial}{\partial \boldsymbol{x}} = [\frac{\partial}{\partial x_1}, \cdots, \frac{\partial}{\partial x_m}]^T \end{array}

  • n×mn \times m 矩阵梯度算子存在两种可能的定义，分别记为：

∇X=[∂∂x11⋯∂∂x1n⋮⋱⋮∂∂xm1⋯∂∂xmn]\begin{array}{c} \nabla_{\boldsymbol{X}} = \left[ \begin{matrix} \frac{\partial}{\partial x_{11}} & \cdots & \frac{\partial}{\partial x_{1n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial}{\partial x_{m1}} & \cdots & \frac{\partial}{\partial x_{mn}} \end{matrix} \right] \end{array}

和

∇vecX=∂∂vecX=[∂∂x11,⋯ ,∂∂xm1,⋯ ,∂∂x1n,⋯ ,∂∂xmn]T\begin{array}{c} \nabla_{\mathrm{vec}\boldsymbol{X}} = \frac{\partial}{\partial_{\mathrm{vec}\boldsymbol{X}}} = [\frac{\partial}{\partial x_{11}}, \cdots, \frac{\partial}{\partial x_{m1}}, \cdots, \frac{\partial}{\partial x_{1n}}, \cdots, \frac{\partial}{\partial x_{mn}}]^T \end{array}

前者称为矩阵变元 X\boldsymbol{X} 的梯度矩阵算子，后者称为梯度向量算子。此二者关系为：

∇vecX=vec(∇X)\begin{array}{c} \nabla_{\mathrm{vec} \boldsymbol{X}} = \mathrm{vec}(\nabla_{\boldsymbol{X}}) \end{array}

由以上定义可知，行向量算子和列向量算子、Jacobian 矩阵算子和梯度矩阵算子、行偏导向量算子和梯度向量算子之间的关系为：

∇x=DxT∇X=DXT∇vecX=DvecXT\begin{array}{c} \nabla_{\boldsymbol{x}} = D_{\boldsymbol{x}}^T \\ \nabla_{\boldsymbol{X}} = D_{\boldsymbol{X}}^T \\ \nabla_{\mathrm{vec}\boldsymbol{X}} = D_{\mathrm{vec}\boldsymbol{X}}^T \end{array}

可以看到，梯度向量等于行偏导向量的转置。在此意义上，行向量偏导向量是列向量形式的梯度向量的协变形式，故又称行偏导向量为协梯度向量。类似地，Jacobian 矩阵也称为协梯度矩阵。

2.4 实值标量函数偏导

  • 实值标量函数 f(x)f(\boldsymbol{x}) 对向量变元 x\boldsymbol{x} 的行向量偏导为：

Dxf(x)=def∂f(x)∂xT=[∂f(x)∂x1,⋯ ,∂f(x)∂xm]\begin{array}{c} D_{\boldsymbol{x}} f(\boldsymbol{x}) \overset{\mathrm{def}}{=} \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}^T} = [\frac{\partial f(\boldsymbol{x})}{\partial x_1}, \cdots, \frac{\partial f(\boldsymbol{x})}{\partial x_m}] \end{array}

  • 实值标量函数 f(x)f(\boldsymbol{x}) 对向量变元 x\boldsymbol{x} 的列向量偏导为：

∇xf(x)=def∂f(x)∂x=[∂f(x)∂x1,⋯ ,∂f(x)∂xm]T\begin{array}{c} \nabla_{\boldsymbol{x}} f(\boldsymbol{x}) \overset{\mathrm{def}}{=} \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}} = [\frac{\partial f(\boldsymbol{x})}{\partial x_1}, \cdots, \frac{\partial f(\boldsymbol{x})}{\partial x_m}]^T \end{array}

  • 实值标量函数 f(X)f(\boldsymbol{X}) 对矩阵变元 X\boldsymbol{X} 的 Jacobian 矩阵为：

DXf(X)=∂f(X)∂XT=[∂f(X)∂x11⋯∂f(X)xm1⋮⋱⋮∂f(X)∂x1n⋯∂f(X)∂xmn]\begin{array}{c} D_{\boldsymbol{X}} f(\boldsymbol{X}) = \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}^T} = \left[ \begin{matrix} \frac{\partial f(\boldsymbol{X})}{\partial x_{11}} & \cdots & \frac{\partial f(\boldsymbol{X})}{x_{m1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f(\boldsymbol{X})}{\partial x_{1n}} & \cdots & \frac{\partial f(\boldsymbol{X})}{\partial x_{mn}} \end{matrix} \right] \end{array}

行偏导向量为：

DrvecXf(X)=[∂∂x11,⋯ ,∂∂xm1,⋯ ,∂∂x1n,⋯ ,∂∂xmn]\begin{array}{c} D_{\mathrm{rvec} \boldsymbol{X}} f(\boldsymbol{X}) = [\frac{\partial}{\partial x_{11}}, \cdots, \frac{\partial}{\partial x_{m1}}, \cdots, \frac{\partial}{\partial x_{1n}}, \cdots, \frac{\partial}{\partial x_{mn}}] \end{array}

  • 实值标量函数 f(X)f(\boldsymbol{X}) 对矩阵变元 X\boldsymbol{X} 的梯度矩阵为：

∇Xf(X)=∂f(X)∂X=[∂f(X)∂x11⋯∂f(X)∂x1n⋮⋱⋮∂f(X)∂xm1⋯∂f(X)∂xmn]\begin{array}{c} \nabla_{\boldsymbol{X}} f(\boldsymbol{X}) = \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}} = \left[ \begin{matrix} \frac{\partial f(\boldsymbol{X})}{\partial x_{11}} & \cdots & \frac{\partial f(\boldsymbol{X})}{\partial x_{1n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f(\boldsymbol{X})}{\partial x_{m1}} & \cdots & \frac{\partial f(\boldsymbol{X})}{\partial x_{mn}} \end{matrix} \right] \end{array}

梯度向量为：

∇vecXf(X)=∂f(X)∂vecX=[∂f(X)∂x11,⋯ ,∂f(X)∂xm1,⋯ ,∂f(X)∂x1n,⋯ ,∂f(X)∂xmn]T\begin{array}{c} \nabla_{\mathrm{vec}\boldsymbol{X}} f(\boldsymbol{X}) = \frac{\partial f(\boldsymbol{X})}{\partial_{\mathrm{vec}\boldsymbol{X}}} = [\frac{\partial f(\boldsymbol{X})}{\partial x_{11}}, \cdots, \frac{\partial f(\boldsymbol{X})}{\partial x_{m1}}, \cdots, \frac{\partial f(\boldsymbol{X})}{\partial x_{1n}}, \cdots, \frac{\partial f(\boldsymbol{X})}{\partial x_{mn}}]^T \end{array}

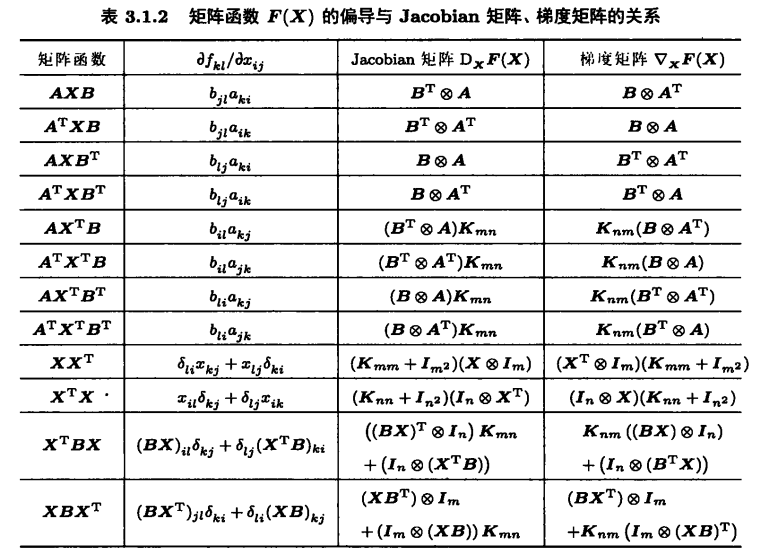
2.5 实值矩阵函数偏导

  • 对于实值矩阵函数 F(X)∈Rp×q \boldsymbol{F}(\boldsymbol{X}) \in \mathbb{R}^{p \times q} ，其中矩阵变元 X∈Rm×n \boldsymbol{X} \in \mathbb{R}^{m \times n} ，Jacobian 矩阵定义为：

DXF(X)=∂vecF(X)∂vecTX\begin{array}{c} D_{\boldsymbol{X}} \boldsymbol{F}(\boldsymbol{X}) = \frac{\partial_{\mathrm{vec}} \boldsymbol{F}(\boldsymbol{X})}{\partial_{\mathrm{vec}^T}\boldsymbol{X}} \end{array}

梯度矩阵定义为：

∇XF(X)=∂vecTF(X)∂vecX\begin{array}{c} \nabla_{\boldsymbol{X}} \boldsymbol{F}(\boldsymbol{X}) = \frac{\partial_{\mathrm{vec}^T} \boldsymbol{F}(\boldsymbol{X})}{\partial_{\mathrm{vec}}\boldsymbol{X}} \end{array}

【注】实值矩阵函数的 Jacobian 矩阵和梯度矩阵与对应偏导的 DX,∇XD_{\boldsymbol{X}}, \nabla_{\boldsymbol{X}} 算子原始定义不相符，但为了保持符号的一致性，仍沿用与实值标量函数相同的算子符号。

3. 性质

3.1 基本法则

  • 若 f(X)=c f(\boldsymbol{X}) = c 为常数，其中 X\boldsymbol{X} 为 m×nm \times n 矩阵，则梯度 ∂c∂X=0m×n \frac{\partial c}{\partial \boldsymbol{X}} = \boldsymbol{0}_{m \times n} 。

  • 线性法则：若 f(X)f(\boldsymbol{X}) 和 g(X)g(\boldsymbol{X}) 分别是矩阵 X\boldsymbol{X} 的实值函数，c1c_1 和 c2c_2 为实常数，则

∂[c1f(X)+c2f(X)]∂X=c1∂f(X)∂X+c2∂g(X)∂X\begin{array}{c} \frac{\partial [c_1 f(\boldsymbol{X}) + c_2 f(\boldsymbol{X})]}{\partial \boldsymbol{X}} = c_1 \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}} + c_2 \frac{\partial g(\boldsymbol{X})}{\partial \boldsymbol{X}} \end{array}

  • 乘积法则：若 f(X)f(\boldsymbol{X}) 、g(X)g(\boldsymbol{X}) 和 h(X)h(\boldsymbol{X}) 都是矩阵 X\boldsymbol{X} 的实值函数，则

∂[f(X)g(X)]∂X=g(X)∂f(X)∂X+f(X)∂g(X)∂X\begin{array}{c} \frac{\partial [f(\boldsymbol{X}) g(\boldsymbol{X})]}{\partial \boldsymbol{X}} = g(\boldsymbol{X}) \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}} + f(\boldsymbol{X}) \frac{\partial g(\boldsymbol{X})}{\partial \boldsymbol{X}} \end{array}

  • 商法则：若 g(X)≠0g(\boldsymbol{X}) \ne 0，则

∂[f(X)/g(X)]∂X=1g2(X)[g(X)∂f(X)∂X−f(X)∂g(X)∂X]\begin{array}{c} \frac{\partial [f(\boldsymbol{X}) / g(\boldsymbol{X})]}{\partial \boldsymbol{X}} = \frac{1}{g^2(\boldsymbol{X})} [ g(\boldsymbol{X}) \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}} - f(\boldsymbol{X}) \frac{\partial g(\boldsymbol{X})}{\partial \boldsymbol{X}} ] \end{array}

  • 链式法则：令 X\boldsymbol{X} 为 m×nm \times n 矩阵，且 y=f(X) y = f(\boldsymbol{X}) 和 g(y)g(y) 分别是以矩阵 X\boldsymbol{X} 和标量 yy 为变元的实值函数，则

∂g(f(X))∂X=dg(y)dy∂f(X)∂X\begin{array}{c} \frac{\partial g(f(\boldsymbol{X}))}{\partial \boldsymbol{X}} = \frac{\mathrm{d}g(y)}{\mathrm{d}y} \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}} \end{array}

推而广之，对实值函数 g(F(X))g(\boldsymbol{F}(\boldsymbol{X}))，其中 F=[fkl]∈Rp×q,X=[xij]∈Rm×n \boldsymbol{F} = [f_{kl}] \in \mathbb{R}^{p \times q}, \boldsymbol{X} = [x_{ij}] \in \mathbb{R}^{m \times n} ，则链式法则为

[∂g(F(X))∂X]ij=∂g(F(X))∂xij=∑k=1p∑l=1q∂g(F(X))∂fkl(X)∂fkl(X)∂xij\begin{array}{c} [\frac{\partial g(\boldsymbol{F}(\boldsymbol{X}))}{\partial \boldsymbol{X}}]_{ij} = \frac{\partial g(\boldsymbol{F}(\boldsymbol{X}))}{\partial x_{ij}} = \sum_{k=1}^p \sum_{l=1}^q \frac{\partial g(\boldsymbol{F}(\boldsymbol{X}))}{\partial f_{kl}(\boldsymbol{X})} \frac{\partial f_{kl}(\boldsymbol{X})}{\partial x_{ij}} \end{array}

3.2 常用性质

  • 对于实值标量函数 f(x)=xTAx f(\boldsymbol{x}) = \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x} ，其中 A∈Rn×n,x∈Rn×1\boldsymbol{A} \in \mathbb{R}^{n \times n}, \boldsymbol{x} \in \mathbb{R}^{n \times 1}，其行偏导向量和矩阵向量为

Dxf(x)=xT(A+AT)∇xf(x)=(AT+A)x\begin{array}{c} D_\boldsymbol{x} f(\boldsymbol{x}) = \boldsymbol{x}^T(\boldsymbol{A} + \boldsymbol{A}^T) \\ \nabla_\boldsymbol{x} f(\boldsymbol{x}) = (\boldsymbol{A}^T + \boldsymbol{A})\boldsymbol{x} \end{array}

  • 对于实值标量函数 f(X)=aTXTXb f(\boldsymbol{X}) = \boldsymbol{a}^T \boldsymbol{X}^T \boldsymbol{X} \boldsymbol{b} ，其中 X∈Rm×n,a,b∈Rn×1 \boldsymbol{X} \in \mathbb{R}^{m \times n}, \boldsymbol{a},\boldsymbol{b} \in \mathbb{R}^{n \times 1} ，其 Jacobian 矩阵和梯度矩阵为

DXf(X)=X(baT+abT)∇Xf(X)=(baT+abT)XT\begin{array}{c} D_{\boldsymbol{X}} f(\boldsymbol{X}) = \boldsymbol{X} (\boldsymbol{b} \boldsymbol{a}^T + \boldsymbol{a} \boldsymbol{b}^T) \\ \nabla_{\boldsymbol{X}} f(\boldsymbol{X}) = (\boldsymbol{b} \boldsymbol{a}^T + \boldsymbol{a} \boldsymbol{b}^T) \boldsymbol{X}^T \end{array}

  • 对于实值矩阵函数 F(X)=X∈Rm×n \boldsymbol{F}(\boldsymbol{X}) = \boldsymbol{X} \in \mathbb{R}^{m \times n} ，其 Jacobian 矩阵和梯度矩阵为

DXF(X)=∇XF(X)=Imn∈Rmn×mn\begin{array}{c} D_{\boldsymbol{X}} \boldsymbol{F} (\boldsymbol{X}) = \nabla_{\boldsymbol{X}} \boldsymbol{F}(\boldsymbol{X}) = \boldsymbol{I}_{mn} \in \mathbb{R}^{mn \times mn} \end{array}

  • 对于实值矩阵函数 F(X)=AXB \boldsymbol{F}(\boldsymbol{X}) = \boldsymbol{A} \boldsymbol{X} \boldsymbol{B} ，其中 A∈Rp×m,X∈Rm×n,B∈Rn×q \boldsymbol{A} \in \mathbb{R}^{p \times m}, \boldsymbol{X} \in \mathbb{R}^{m \times n}, \boldsymbol{B} \in \mathbb{R}^{n \times q} ，其 Jacobian 矩阵和梯度矩阵为

DXF(X)=BT⊗A∇XF(X)=B⊗AT\begin{array}{c} D_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X}) = \boldsymbol{B}^T \otimes \boldsymbol{A} \\ \nabla_{\boldsymbol{X}} \boldsymbol{F}(\boldsymbol{X}) = \boldsymbol{B} \otimes \boldsymbol{A}^T \end{array}

  • 在机器学习中，对于线性实值矩阵函数 Y=X⋅W+b \boldsymbol{Y} = \boldsymbol{X} \cdot \boldsymbol{W} + \boldsymbol{b} ，其中 X∈Rn×m,W∈Rm×1,b∈Rn×1 \boldsymbol{X} \in \mathbb{R}^{n \times m}, \boldsymbol{W} \in \mathbb{R}^{m \times 1}, \boldsymbol{b} \in \mathbb{R}^{n \times 1} ，损失函数为 L\mathcal{L}，则有梯度

[∇XL]kl=[∂L∂X]kl=∑i=1n∂L∂yi∂yi∂xkl=wl∂L∂yk⇓∇XL=∂L∂X=∂L∂YWT\begin{array}{c} [\nabla_{\boldsymbol{X}} \mathcal{L}]_{kl} = [\frac{\partial \mathcal{L}}{\partial \boldsymbol{X}}]_{kl} = \sum_{i=1}^n \frac{\partial \mathcal{L}}{\partial y_{i}} \frac{\partial y_{i}}{\partial x_{kl}} = w_{l} \frac{\partial \mathcal{L}}{\partial y_k} \\ \Downarrow \\ \nabla_{\boldsymbol{X}} \mathcal{L} = \frac{\partial \mathcal{L}}{\partial \boldsymbol{X}} = \frac{\partial \mathcal{L}}{\partial \boldsymbol{Y}} \boldsymbol{W}^T \end{array}

类似地，有

[∇WL]k=[∂L∂W]k=∑i=1n∂L∂yi∂yi∂wk=∑i=1n∂L∂yixik⇓∇WL=∂L∂W=XT∂L∂Y\begin{array}{c} [\nabla_{\boldsymbol{W}} \mathcal{L}]_{k} = [\frac{\partial \mathcal{L}}{\partial \boldsymbol{W}}]_{k} = \sum_{i=1}^n \frac{\partial \mathcal{L}}{\partial y_{i}} \frac{\partial y_{i}}{\partial w_{k}} = \sum_{i=1}^n \frac{\partial \mathcal{L}}{\partial y_i} x_{ik} \\ \Downarrow \\ \nabla_{\boldsymbol{W}} \mathcal{L} = \frac{\partial \mathcal{L}}{\partial \boldsymbol{W}} = \boldsymbol{X}^T \frac{\partial \mathcal{L}}{\partial \boldsymbol{Y}} \end{array}

4. 常用公式

4.1 向量函数及其偏导

向量函数 偏导
axa \boldsymbol{x} aIa \boldsymbol{I}
bTx\boldsymbol{b}^T \boldsymbol{x} b\boldsymbol{b}
xTb\boldsymbol{x}^T \boldsymbol{b} b\boldsymbol{b}
xTx\boldsymbol{x}^T \boldsymbol{x} 2x2 \boldsymbol{x}
xxT\boldsymbol{x} \boldsymbol{x}^T I⊗x+x⊗I\boldsymbol{I} \otimes \boldsymbol{x} + \boldsymbol{x} \otimes \boldsymbol{I}
bTAx\boldsymbol{b}^T \boldsymbol{A} \boldsymbol{x} ATb\boldsymbol{A}^T \boldsymbol{b}
xTAb\boldsymbol{x}^T \boldsymbol{A} \boldsymbol{b} Ab\boldsymbol{A} \boldsymbol{b}
xTAx\boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x} (A+AT)x(\boldsymbol{A} + \boldsymbol{A}^T) \boldsymbol{x}
exp⁡(−12xTAx)\exp{(-\frac{1}{2} \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x})} −12(A+AT)x⋅exp⁡(−12xTAx)-\frac{1}{2} (\boldsymbol{A} + \boldsymbol{A}^T) \boldsymbol{x} \cdot \exp{(-\frac{1}{2} \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x})}

4.2 矩阵函数及其偏导

Technique Math Theory 矩阵
Technique 数学 Math Theory 矩阵

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！