【注】本文采用 PyTorch 框架，基于 Fashion-MNIST 数据集。

1. LeNet

LeNet分为卷积层块和全连接层块两个部分。

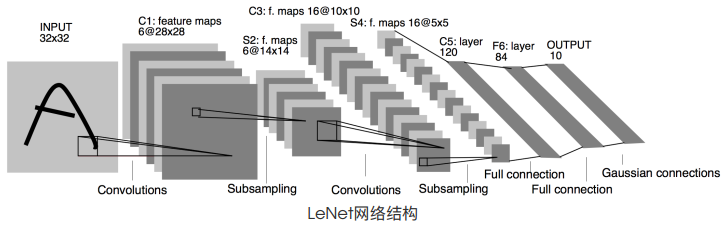
1.1 卷积层块

• 卷积层块⾥的基本单位是卷积层后接最⼤池化层：卷积层⽤来识别图像⾥的空间模式，如线条和物体局部，之后的最⼤池化层则⽤来降低卷积层对位置的敏感性。

• 在卷积层块中：每个卷积层都使⽤ $5 \times 5$ 的窗⼝，并在输出上使⽤ sigmoid 激活函数。第⼀个卷积层输出通道数为 6 ，第⼆个卷积层输出通道数则增加到 16 。这是因为第⼆个卷积层⽐第⼀个卷积层的输⼊的⾼和宽要⼩，所以增加输出通道使两个卷积层的参数尺⼨类似。

• 卷积层块的两个最⼤池化层的窗⼝形状均为 $2 \times 2$，且步幅为 2 。由于池化窗⼝与步幅形状相同，池化窗⼝在输⼊上每次滑动所覆盖的区域互不重叠。

• 卷积层块的输出形状为(批量⼤⼩, 通道, ⾼, 宽)。

1.2 全连接层块

• 当卷积层块的输出传⼊全连接层块时，全连接层块会将⼩批量中每个样本变平（flatten）。也就是说，全连接层的输⼊形状将变成⼆维，其中第⼀维是⼩批量中的样本，第⼆维是每个样本变平后的向量表示，且向量⻓度为通道、⾼和宽的乘积。

• 全连接层块含 3 个全连接层。它们的输出个数分别是 120、84 和 10 ，其中 10 为输出的类别个数。

1.3 PyTorch 实现

import torch 
import torch.nn as nn 
import torch.optim as optim 
import torchvision
import torchvision.transforms as transforms

# 定义 LeNet 网络
class LeNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 6, 5),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2),
            nn.Conv2d(6, 16, 5),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2)
        )
        self.fc = nn.Sequential(
            nn.Linear(16*4*4, 120),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output

2. AlexNet

AlexNet 与 LeNet 的设计理念⾮常相似，但也有显著的区别。

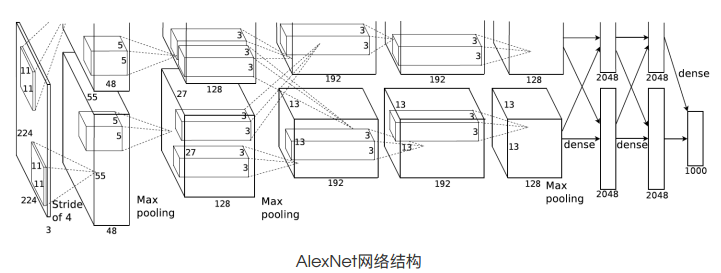
2.1 网络结构

• AlexNet 包含 8 层变换，其中有 5 层卷积和 2 层全连接隐藏层，以及 1 个全连接输出层。

• AlexNet 将 sigmoid 激活函数改成了更加简单的 ReLU 激活函数。

• AlexNet 通过 Dropout 来控制全连接层的模型复杂度。

2.2 PyTorch 实现

import torch 
import torch.nn as nn
import torch.optim as optim 
import torchvision 
import torchvision.transforms as transforms 

# 定义 AlexNet
class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()
        # 卷积层块
        self.conv = nn.Sequential(
            nn.Conv2d(1, 96, 11, 4),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            nn.Conv2d(96, 256, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            nn.Conv2d(256, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
        # 全连接层块
        self.fc = nn.Sequential(
            nn.Linear(256*5*5, 1024),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(1024, 1024),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(1024, 10)
        )
    
    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output 

3. VGG

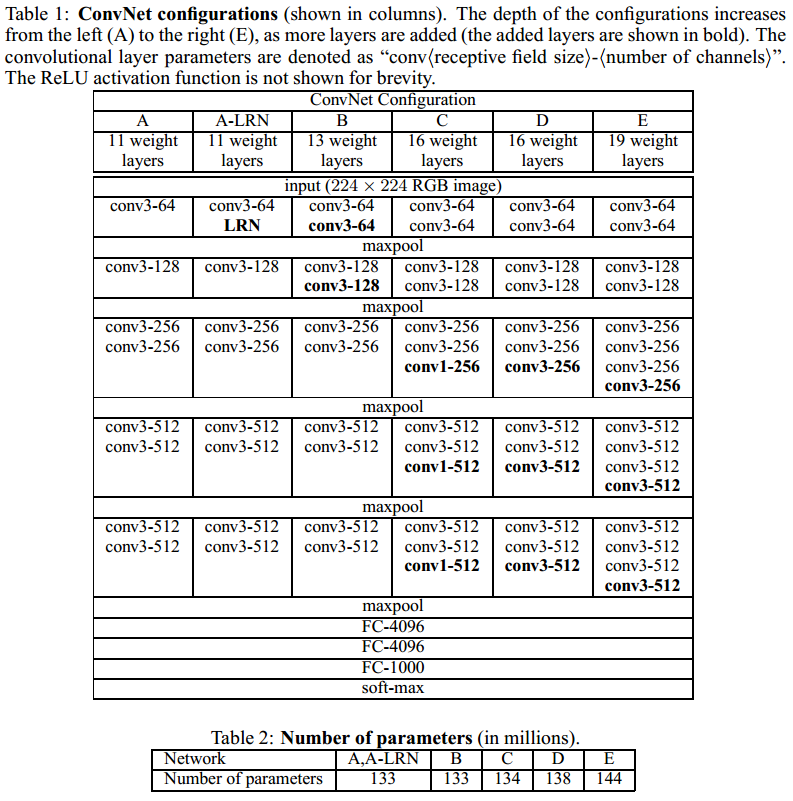
3.1 网络结构

• VGG块的组成规律是：连续使⽤数个相同的填充为1、窗⼝形状为 $3 \times 3$ 的卷积层后接上⼀个步幅为2、窗⼝形状为 $2 \times 2$ 的最⼤池化层。

• 对于给定的感受野（与输出有关的输⼊图⽚的局部⼤⼩），采⽤堆积的⼩卷积核优于采⽤⼤的卷积核，因为可以增加⽹络深度来保证学习更复杂的模式，⽽且代价还⽐较⼩（参数更少）。在 VGG 中，使⽤了 3 个 $3 \times 3$ 卷积核来代替 $7 \times 7$ 卷积核，使⽤了 2 个 $3 \times 3$ 卷积核来代替 $5 \times 5$ 卷积核。

3.2 PyTorch 实现

以下实现了一个简单的 VGG-11 网络。

import torch 
import torch.nn as nn
import torch.optim as optim 
import torchvision 
import torchvision.transforms as transforms 

# 定义网络模型
class VGG(nn.Module):
    def __init__(self):
        super(VGG, self).__init__()
        # 卷积层
        self.vgg_block = nn.Sequential(
            # vgg_block_1
            nn.Conv2d(1, 32, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(2, 2),
            # vgg_block_2
            nn.Conv2d(32, 64, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(2, 2),
            # vgg_block_3
            nn.Conv2d(64, 128, 3, 1, 1),
            nn.Conv2d(128, 128, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(2, 2),
            # vgg_block_4
            nn.Conv2d(128, 256, 3, 1, 1),
            nn.Conv2d(256, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(2, 2),
            # vgg_block_5
            nn.Conv2d(256, 256, 3, 1, 1),
            nn.Conv2d(256, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(2, 2) 
        )
        # 全连接层
        self.fc_block = nn.Sequential(
            nn.Flatten(),
            nn.Linear(256*7*7, 1024),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(1024, 1024),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(1024, 10)         
        )
    
    def forward(self, X):
        vgg = self.vgg_block(X)
        fc = self.fc_block(vgg)
        return fc

4. NiN

4.1 网络结构

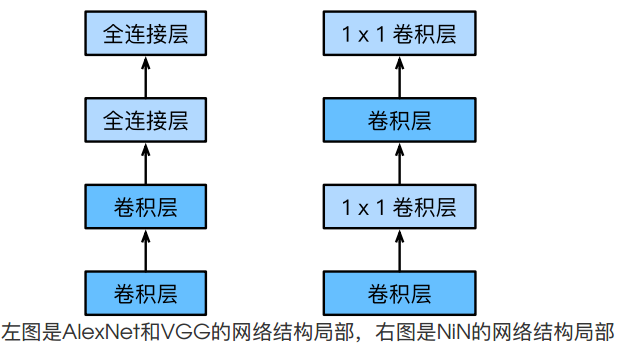
• NiN 使⽤ $1 \times 1$ 的卷积层来替代全连接层。

• NiN 块是 NiN 中的基础块。它由⼀个卷积层加两个充当全连接层的 $1 \times 1$ 卷积层串联⽽成。其中第⼀个卷积层的超参数可以⾃⾏设置，⽽第⼆和第三个卷积层的超参数⼀般是固定的。

• NiN 去掉了 AlexNet 最后的 3 个全连接层，取⽽代之地，NiN 使⽤了输出通道数等于标签类别数的 NiN 块，然后使⽤全局平均池化层对每个通道中所有元素求平均并直接⽤于分类。

4.2 PyTorch 实现

import torch 
import torch.nn as nn
import torch.optim as optim 
import torchvision 
import torchvision.transforms as transforms 

# 定义网络模型
class NiN(nn.Module):
    def __init__(self):
        super(NiN, self).__init__()
        # 定义 NiN 块
        def nin_block(in_channels, out_channels, kernel_size, stride, padding):
            blk = nn.Sequential(
                nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding),
                nn.ReLU(),
                nn.Conv2d(out_channels, out_channels, kernel_size=1),
                nn.ReLU(),
                nn.Conv2d(out_channels, out_channels, kernel_size=1),
                nn.ReLU(),
            )
            return blk 

        self.nin = nn.Sequential(
            nin_block(1, 96, 11, 4, 0),
            nn.MaxPool2d(3, 2),
            nin_block(96, 256, 5, 1, 2),
            nn.MaxPool2d(3, 2),
            nin_block(256, 384, 3, 1, 1),
            nn.MaxPool2d(3, 2),
            nn.Dropout(0.5),
            nin_block(384, 10, 3, 1, 1),
            nn.AvgPool2d(5),
            nn.Flatten(1, -1),
        )
    
    def forward(self, X):
        output = self.nin(X)
        return output 

5. GoogLeNet

5.1 网络结构

GoogLeNet 引入了并行连结的网络结构，其基础卷积块称为 Inception 块，其结构如下：

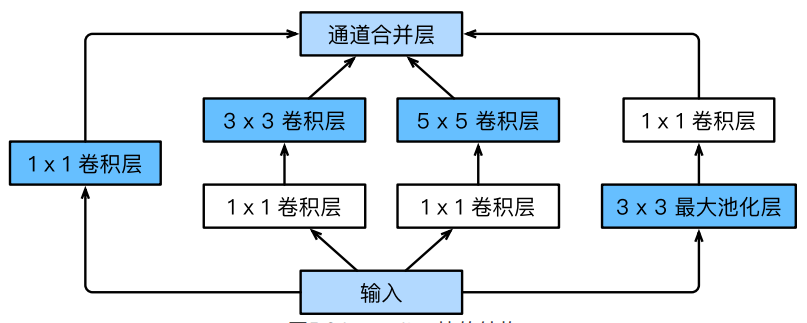
• Inception 块⾥有 4 条并⾏的线路。
• 前 3 条线路使⽤窗⼝⼤⼩分别是 1 \time 1、$3 \times 3$ 和 $5 \times 5$ 的卷积层来抽取不同空间尺⼨下的信息，其中中间 2 个线路会对输⼊先做 $1 \times 1$ 卷积来减少输⼊通道数，以降低模型复杂度。
• 第 4 条线路则使⽤ $3 \times 3$ 最⼤池化层，后接 $1 \times 1$ 卷积层来改变通道数。
• 4 条线路都使⽤了合适的填充来使输⼊与输出的⾼和宽⼀致。最后我们将每条线路的输出在通道维上连结，并输⼊接下来的层中去。

GoogLeNet 跟 VGG ⼀样，在主体卷积部分中使⽤ 5 个模块（block），每个模块之间使⽤步幅为2的 $3 \times 3$ 最⼤池化层来减⼩输出⾼宽。

5.2 PyTorch 实现

import torch 
import torch.nn as nn
import torch.optim as optim 
import torch.nn.functional as F
import torchvision 
import torchvision.transforms as transforms 

# 定义 GlobalAvgPool2d 层
class GlobalAvgPool2d(nn.Module):
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    
    def forward(self, X):
        return F.avg_pool2d(X, kernel_size=X.size()[2:])

# 定义 Inception 块
class Inception(nn.Module):
    def __init__(self, in_c, c1, c2, c3, c4):
        super(Inception, self).__init__()
        # 线路 1 ：单 1 x 1 卷积层
        self.p1_1 = nn.Conv2d(in_c, c1, 1)
        # 线路 2 ：1 x 1 卷积层后接 3 x 3 卷积层
        self.p2_1 = nn.Conv2d(in_c, c2[0], 1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], 3, 1, 1)
        # 线路 3 ：1 x 1 卷积层后接 5 x 5 卷积层
        self.p3_1 = nn.Conv2d(in_c, c3[0], 1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], 5, 1, 2)
        # 线路 4 ：3 x 3 最大池化后接 1 x 1 卷积层
        self.p4_1 = nn.MaxPool2d(3, 1, 1)
        self.p4_2 = nn.Conv2d(in_c, c4, 1)

    def forward(self, X):
        p1 = F.relu(self.p1_1(X))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(X))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(X))))
        p4 = F.relu(self.p4_2(self.p4_1(X)))
        return torch.cat((p1, p2, p3, p4), dim=1)

# 定义网络模型
class GoogLeNet(nn.Module):
    def __init__(self):
        super(GoogLeNet, self).__init__()
        self.googlenet = nn.Sequential(
            # 第一模块
            nn.Conv2d(1, 64, 7, 2, 3),
            nn.ReLU(),
            nn.MaxPool2d(3, 2, 1),
            # 第二模块
            nn.Conv2d(64, 64, 1),
            nn.Conv2d(64, 192, 3, 1),
            nn.MaxPool2d(3, 2, 1), 
            Inception(192, 64, (96, 128), (16, 32), 32),
            Inception(256, 128, (128, 192), (32, 96), 64),
            nn.MaxPool2d(3, 2, 1),
            # 第三模块
            Inception(480, 192, (96, 208), (16, 48), 64),
            Inception(512, 160, (112, 224), (24, 64), 64),
            Inception(512, 128, (128, 256), (24, 64), 64),
            Inception(512, 112, (144, 288), (32, 64), 64),
            Inception(528, 256, (160, 320), (32, 128), 128),
            nn.MaxPool2d(3, 2, 1),
            # 第四模块
            Inception(832, 256, (160, 320), (32, 128), 128),
            Inception(832, 384, (192, 384), (48, 128), 128),
            GlobalAvgPool2d(),
            # 输出层
            nn.Flatten(1, -1),
            nn.Linear(1024, 10),
        )
    
    def forward(self, X):
        output = self.googlenet(X)
        return output 

6. ResNet

6.1 网络结构

ResNet 引入了恒等映射的跨层连结，其基础块称为残差块（Residual），如下所示：

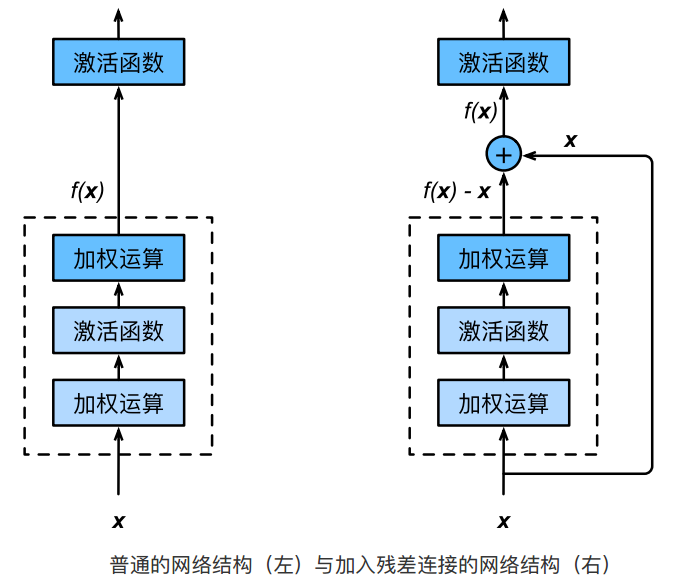
• ResNet 沿⽤了 VGG 全 $3 \times 3$ 卷积层的设计。残差块⾥⾸先有 2 个有相同输出通道数的 $3 \times 3$ 卷积层。每个卷积层后接⼀个批量归⼀化层和 ReLU 激活函数。
• 然后我们将输⼊跳过这两个卷积运算后直接加在最后的 ReLU 激活函数前。这样的设计要求两个卷积层的输出与输⼊形状⼀样，从⽽可以相加。
• 如果想改变通道数，就需要引⼊⼀个额外的 $1 \times 1$ 卷积层来将输⼊变换成需要的形状后再做相加运算。

GoogLeNet 在后⾯接了 4 个由 Inception 块组成的模块。ResNet 则使⽤ 4 个由残差块组成的模块，每个模块使⽤若⼲个同样输出通道数的残差块。

6.2 PyTorch 实现

import torch 
import torch.nn as nn
import torch.optim as optim 
import torch.nn.functional as F
import torchvision 
import torchvision.transforms as transforms 

# 定义 GlobalAvgPool2d 层
class GlobalAvgPool2d(nn.Module):
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    
    def forward(self, X):
        return F.avg_pool2d(X, kernel_size=X.size()[2:])

# 定义 Residual 块
class Residual(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, XconvX=False):
        super(Residual, self).__init__()
        self.residual = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, stride, 1),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(),
            nn.Conv2d(out_channels, out_channels, 3, 1, 1),
            nn.BatchNorm2d(out_channels),
        )
        if XconvX:
            self.XconvX = nn.Conv2d(in_channels, out_channels, 1, stride) 
        else: 
            self.XconvX = None

    def forward(self, X):
        Y = self.residual(X)
        if self.XconvX:
            X = self.XconvX(X)
        return F.relu(Y + X)

# 定义网络模型
class ResNet(nn.Module):
    def __init__(self):
        super(ResNet, self).__init__()
        self.resnet = nn.Sequential(
            # 输入层
            nn.Conv2d(1, 64, 7, 2, 3),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            nn.MaxPool2d(3, 2, 1),
            # 第一模块
            Residual(64, 64, 1),
            Residual(64, 64, 1),
            # 第二模块
            Residual(64, 128, 2, True),
            Residual(128, 128, 1), 
            # 第三模块
            Residual(128, 256, 2, True),
            Residual(256, 256, 1),
            # 第四模块
            Residual(256, 512, 2, True),
            Residual(512, 512, 1),
            # 输出层
            GlobalAvgPool2d(),
            nn.Flatten(1, -1),
            nn.Linear(512, 10),
        )
    
    def forward(self, X):
        output = self.resnet(X)
        return output 

7. DenseNet

7.1 网络结构

DenseNet 的主要局部结构如下：

DenseNet 网络结构如下：

DenseNet 的基础块称为稠密块（DenseBlock）和过渡层（TransitionLayer）：

• 前者定义了输⼊和输出是如何连结的，后者则⽤来控制通道数，使之不过⼤。
• 稠密块由多个「批量归一化、激活和卷积」结构构成，其中卷积块的通道数控制了输出通道数相对于输⼊通道数的增⻓，因此也被称为增⻓率（growth rate）。
• 过渡层通过 $1 \times 1$ 卷积层来减⼩通道数，并使⽤步幅为 2 的平均池化层减半⾼和宽，从⽽进⼀步降低模型复杂度。

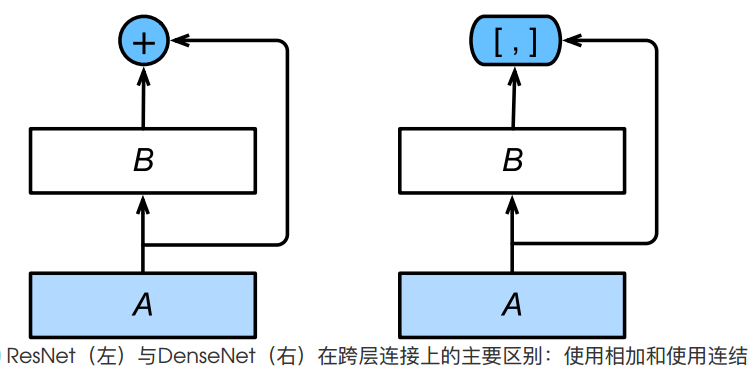
DenseNet 与 ResNet 的主要区别在于：

• 首先，DenseNet ⾥模块的输出不是像 ResNet 那样残差映射 B 和恒等映射 A 相加后输出，⽽是在通道维上将二者连接后输出。
• 其次，在一个 DenseBlock 中，DenseNet 中恒等映射 A 直接和残差映射 B 后的所有层连接在了一起，故称为「稠密连接」。

7.2 PyTorch 实现

import torch 
import torch.nn as nn
import torch.optim as optim 
import torch.nn.functional as F
import torchvision 
import torchvision.transforms as transforms 

# 定义 GlobalAvgPool2d 层
class GlobalAvgPool2d(nn.Module):
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    
    def forward(self, X):
        return F.avg_pool2d(X, kernel_size=X.size()[2:])

# 定义批量归一化、激活和卷积结构
def conv_block(in_channels, out_channels):
    blk = nn.Sequential(
        nn.BatchNorm2d(in_channels),
        nn.ReLU(),
        nn.Conv2d(in_channels, out_channels, 3, 1, 1)
    )
    return blk 

# 定义 DenseBlock 块
class DenseBlock(nn.Module):
    def __init__(self, in_channels, out_channels, num_convs):
        super(DenseBlock, self).__init__()
        dense_block = []
        for i in range(num_convs):
            in_c = in_channels + i*out_channels 
            dense_block.append(conv_block(in_c, out_channels))
        self.dense_block = nn.ModuleList(dense_block)
        self.out_channels = in_channels + num_convs*out_channels

    def forward(self, X):
        for blk in self.dense_block:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)
        return X 

# 定义 TransitionBlock 块
class TransitionBlock(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(TransitionBlock, self).__init__()
        self.transition_block = nn.Sequential(
            nn.BatchNorm2d(in_channels),
            nn.ReLU(),
            nn.Conv2d(in_channels, out_channels, 1, 1, 0),
            nn.AvgPool2d(2, 2),
        )

    def forward(self, X):
        output = self.transition_block(X)
        return output

# 定义网络模型
class DenseNet(nn.Module):
    def __init__(self):
        super(DenseNet, self).__init__()
        self.dense_net = nn.Sequential()
        self.dense_net.add_module(
            'InputLayer',
            nn.Sequential(
                # 输入层
                nn.Conv2d(1, 64, 7, 2, 3),
                nn.BatchNorm2d(64),
                nn.ReLU(),
                nn.MaxPool2d(3, 2, 1),
            )
        )
        # 中间 4 个稠密块 + 3 个过渡层
        num_channels, growth_rate = 64, 32 
        num_convs_in_dense_block = [4, 4, 4, 4]
        for i, num_convs in enumerate(num_convs_in_dense_block):
            # 稠密块
            dense_block = DenseBlock(num_channels, growth_rate, num_convs)
            self.dense_net.add_module('DenseBlock %d' % i, dense_block)
            num_channels = dense_block.out_channels 
            if i != len(num_convs_in_dense_block) - 1:
                # 过渡层
                self.dense_net.add_module('TransitionBlock %d' % i, TransitionBlock(num_channels, num_channels // 2))
                num_channels = num_channels // 2 
        self.dense_net.add_module(
            'OutputLayer',
            nn.Sequential(
                # 输出层
                nn.BatchNorm2d(num_channels),
                nn.ReLU(),
                GlobalAvgPool2d(),
                nn.Flatten(1, -1),
                nn.Linear(num_channels, 10),
            )
        )

    def forward(self, X):
        output = self.dense_net(X)
        return output