概述

1. 定义

监督学习方法可以为生成方法和判别方法，所学到的模型分别称为生成模型和判别模型。

  • 生成方法由数据学习联合概率分布 P(X,Y)P(X, Y)，然后求出条件概率分布 P(Y∣X)P(Y | X) 作为预测的模型，即生成模型：

    P(Y∣X)=P(X,Y)P(X)P(Y | X) = \frac{P(X, Y)}{P(X)}

    生成模型表示了给定输入 XX 产生输出 YY 的生成关系。典型的生成模型有朴素贝叶斯法和隐马尔可夫模型。

  • 判别方法由数据直接学习决策函数 f(X)f(X) 或者条件概率分布 P(Y∣X)P(Y | X) 作为预测的模型，即判别模型。判别方法关心的是对给定的输入 XX，应该预测什么样的输出 YY。典型的判别模型有：kk 近邻法、感知机、决策树、逻辑斯谛回归模型、最大熵模型、支持向量机、提升方法和条件随机场等。

监督学习的应用主要在三个方面：分类问题、标注问题和回归问题。

2. 分类问题

分类问题主要包括学习和分类两个过程：

  • 在学习过程中，根据已知的训练数据集利用有效的学习方法学习一个分类器；
  • 在分类过程中，利用学习的分类器对新的输入实例进行分类。

学习系统由训练数据学习一个分类器 P(Y∣X)P(Y | X) 或 Y=f(X)Y = f(X)，并使用该分类器对新的输入例 xN+1x_{N+1} 进行分类预测。

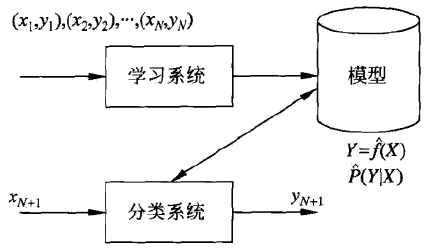
评价分类器性能的指标一般是分类准确度（accuracy），其定义是：对于给定测试数据集，分类器正确分类的样本数与总样本数之比。

对于二类分类问题，常用的评价指标是精确率（precision）与召回率（recall）。通常以关注的类为正类，其他类为负类，分类器在测试数据集上的预测或正确或不正确，44 种情况出现的总数分别记作：

  • TPTP：将正类预测为正类数；
  • FNFN：将正类预测为负类数；
  • FPFP：将负类预测为正类数；
  • TNTN：将负类预测为负类数。

则精确率定义为：

P=TPTP+FPP = \frac{TP}{TP + FP}

召回率定义为：

R=TPTP+FNR = \frac{TP}{TP + FN}

此外，常用的还有 F1F_1 值，其为精确率和召回率的调和均值，定义为：

2F1=1P+1RF1=2TP2TP+FP+FN\frac{2}{F_1} = \frac{1}{P} + \frac{1}{R} \\ F_1 = \frac{2TP}{2TP + FP + FN}

精确率和召回率都高时，F1F_1 值也会很高。

3. 标注问题

标注问题的输入是一个观测序列，输出是一个标记序列或状态序列。标注问题的目标在于学习一个模型，使它能够对观测序列给出标记序列作为预测。

  • 训练数据集 T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}，其中xi=(xi(1),xi(2),⋯ ,xi(n))⊤,i=1,2,⋯ ,Nx_{i}=(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(n)})^{\top}, i=1,2, \cdots, N 是输入序列，yi=(yi(1),yi(2),⋯ ,yi(n))⊤y_{i}=(y_{i}^{(1)}, y_{i}^{(2)}, \cdots, y_{i}^{(n)})^{\top}是相应的输出序列，nn 是序列长度，一般 n≪Nn \ll N。

学习系统基于构建一个模型，表示为条件概率分布：

P(Y(1),Y(2),⋯ ,Y(n)∣X(1),X(2),⋯ ,X(n))P\left(Y^{(1)}, Y^{(2)}, \cdots, Y^{(n)} \mid X^{(1)}, X^{(2)}, \cdots, X^{(n)}\right)

并对新的输入序列 xN+1=(xN+1(1),xN+1(2),⋯ ,xN+1(n))⊤x_{N+1}=(x_{N+1}^{(1)}, x_{N+1}^{(2)}, \cdots, x_{N+1}^{(n)})^{\top} 给出使条件概率 P((yN+1(1),yN+1(2),⋯ ,yN+1(n))⊤∣(xN+1(1),xN+1(2),⋯ ,xN+1(n))⊤)P\left((y_{N+1}^{(1)}, y_{N+1}^{(2)}, \cdots, y_{N+1}^{(n)})^\top | (x_{N+1}^{(1)}, x_{N+1}^{(2)}, \cdots, x_{N+1}^{(n)})^\top\right) 最大的标记序列 yN+1=(yN+1(1),yN+1(2),⋯ ,yN+1(n))⊤y_{N+1} = (y_{N+1}^{(1)}, y_{N+1}^{(2)}, \cdots, y_{N+1}^{(n)})^\top 作为预测。

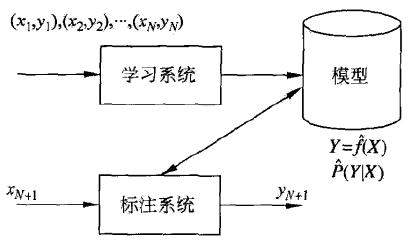
评价标注模型的指标与评价分类模型的指标一样。

4. 回归问题

回归用于预测输入变量要（自变量）和输出变量（因变量）之间的关系。回归模型是表示输入变量到输出变量之间映射的函数。回归问题的学习等价于函数拟合：选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。

  • 训练数据集 T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}，其中 xi∈Rnx_{i} \in \mathbf{R}^{n} 为输入，y∈Ry \in \mathbf{R} 是对应的输出，i=1,2,⋯ ,Ni = 1, 2, \cdots, N。

学习系统基于训练数据构建一个模型，即函数 Y=f(X)Y = f(X)，对于新的输入 xN+1x_{N+1}，预测系统根据学习的模型 Y=f(X)Y = f(X) 确实相应的输出yN+1y_{N+1}。

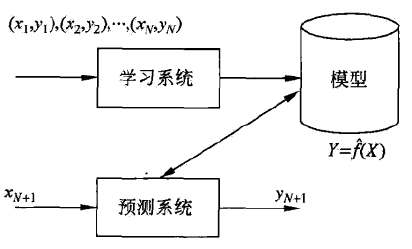
回归问题按照输入变量的个数，分为一元回归和多元回归；按照输入变量和要输出变量之间关系的类型（也即模型的类型），分为线性回归和非线性回归。

附录

  • 《统计学习方法》by 李航