1. 模运算
1.1 Z n Z_n Z n
模加运算:( a + b ) m o d n = c (a+b) \mod \ n = c ( a + b ) m o d n = c
模减运算:( a − b ) m o d n = c (a-b) \mod \ n = c ( a − b ) m o d n = c
模乘运算:( a × b ) m o d n = c (a \times b) \mod \ n = c ( a × b ) m o d n = c
1.2 Z n Z_n Z n
[ ( a m o d n ) + ( b m o d n ) ] m o d n = ( a + b ) m o d n [(a \mod \ n) + (b \mod \ n)] \mod \ n = (a + b) \mod \ n [ ( a m o d n ) + ( b m o d n ) ] m o d n = ( a + b ) m o d n [ ( a m o d n ) − ( b m o d n ) ] m o d n = ( a − b ) m o d n [(a \mod \ n) - (b \mod \ n)] \mod \ n = (a - b) \mod \ n [ ( a m o d n ) − ( b m o d n ) ] m o d n = ( a − b ) m o d n [ ( a m o d n ) × ( b m o d n ) ] m o d n = ( a × b ) m o d n [(a \mod \ n) \times (b \mod \ n)] \mod \ n = (a \times b) \mod \ n [ ( a m o d n ) × ( b m o d n ) ] m o d n = ( a × b ) m o d n
1.3 扩展欧几里得求 Z n Z_n Z n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int exgcd (int a, int b, int & x, int & y) int ans = 0 ;if (b == 0 ) {1 ;0 ;else {exgcd (b,a%b,x,y);int t = x;return ans;
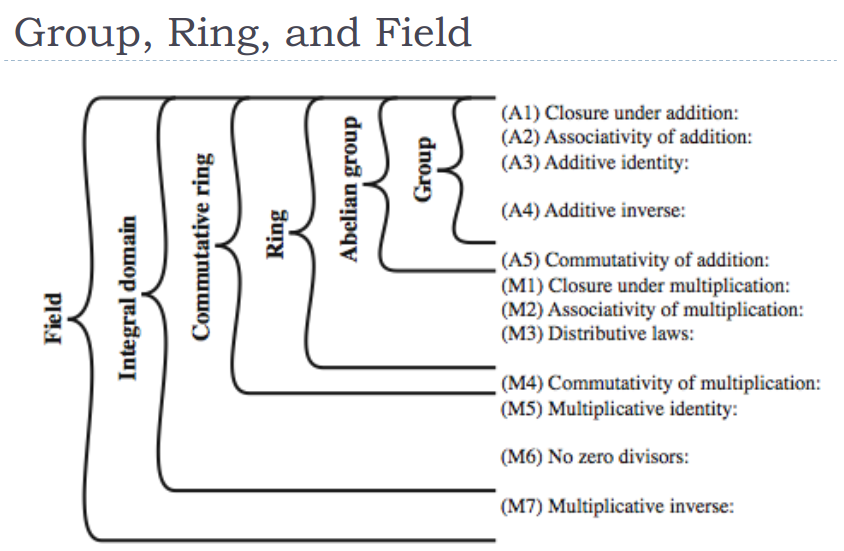
2. 群环域
3. 伽罗瓦域
3.1 G F ( 2 ) GF(2) G F ( 2 )
0 + 0 = 0
0 – 0 = 0
0 + 1 = 1
1 – 0 = 1
1 + 0 = 1
0 – 1 = 0 + 1 = 1
1 + 1 = 0
1 – 1 = 1 + 1 = 0
0 × \times ×
0 × \times ×
1 × \times ×
1 × \times ×
3.2 G F ( 2 n ) GF(2^n) G F ( 2 n )
G F ( 2 n ) GF(2^n) G F ( 2 n ) 每个元素的加法逆是其本身
AES 中用到了 G F ( 2 8 ) GF(2^8) G F ( 2 8 )
m ( x ) = x 8 + x 4 + x 3 + x + 1 \begin{array}{c}
m(x) = x^8 + x^4 + x^3 + x + 1
\end{array}
m ( x ) = x 8 + x 4 + x 3 + x + 1
根据长除法可得:
x 8 m o d m ( x ) = x 4 + x 3 + x + 1 x 8 m o d m ( x ) = 00011011 \begin{array}{c}
x^8 \mod \ m(x) = x^4 + x^3 + x + 1 \\
x^8 \mod \ m(x) = 00011011
\end{array}
x 8 m o d m ( x ) = x 4 + x 3 + x + 1 x 8 m o d m ( x ) = 0 0 0 1 1 0 1 1
对于一个多项式
f ( x ) = b 7 x 7 + b 6 x 6 + b 5 x 5 + b 4 x 4 + b 3 x 3 + b 2 x 2 + b 1 x + b 0 \begin{array}{c}
f(x) = b_7x^7 + b_6x^6 + b_5x^5 + b_4x^4 + b_3x^3 + b_2x^2 + b_1x + b_0
\end{array}
f ( x ) = b 7 x 7 + b 6 x 6 + b 5 x 5 + b 4 x 4 + b 3 x 3 + b 2 x 2 + b 1 x + b 0
其对应的位模式为
f ( x ) = b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 \begin{array}{c}
f(x) = b_7b_6b_5b_4b_3b_2b_1b_0
\end{array}
f ( x ) = b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0
则 x f ( x ) xf(x) x f ( x )
x f ( x ) = 00000010 ⋅ f ( x ) = { b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 i f b 7 = 0 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 ⊕ 00011011 i f b 7 = 1 \begin{array}{c}
xf(x) = 00000010 \cdot f(x) =
\begin{cases}
b_6b_5b_4b_3b_2b_1b_00 & if \ b_7 = 0 \\
b_6b_5b_4b_3b_2b_1b_00 \oplus 00011011 & if \ b_7 = 1
\end{cases}
\end{array}
x f ( x ) = 0 0 0 0 0 0 1 0 ⋅ f ( x ) = { b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 ⊕ 0 0 0 1 1 0 1 1 i f b 7 = 0 i f b 7 = 1
而对于 x 2 f ( x ) x^2f(x) x 2 f ( x ) x 3 f ( x ) x^3f(x) x 3 f ( x ) ⋯ \cdots ⋯ x 7 f ( x ) x^7f(x) x 7 f ( x )
x 2 f ( x ) = x ( x f ( x ) ) x 3 f ( x ) = x ( x 2 f ( x ) ) ⋮ x 7 f ( x ) = x ( x 6 f ( x ) ) \begin{array}{c}
x^2f(x) = x(xf(x)) \\
x^3f(x) = x(x^2f(x)) \\
\vdots \\
x^7f(x) = x(x^6f(x))
\end{array}
x 2 f ( x ) = x ( x f ( x ) ) x 3 f ( x ) = x ( x 2 f ( x ) ) ⋮ x 7 f ( x ) = x ( x 6 f ( x ) )
由此,可以通过将 f ( x ) ⋅ g ( x ) f(x) \cdot g(x) f ( x ) ⋅ g ( x ) f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) g ( x ) g(x) g ( x )
b 7 ⋅ 2 7 + b 6 ⋅ 2 6 + b 5 ⋅ 2 5 + b 4 ⋅ 2 4 + b 3 ⋅ 2 3 + b 2 ⋅ 2 2 + b 1 ⋅ 2 1 + b 0 ⋅ 2 0 \begin{array}{c}
b_7 \cdot 2^7 + b_6 \cdot 2^6 + b_5 \cdot 2^5 + b_4 \cdot 2^4 + b_3 \cdot 2^3 + b_2 \cdot 2^2 + b_1 \cdot 2^1 + b_0 \cdot 2^0
\end{array}
b 7 ⋅ 2 7 + b 6 ⋅ 2 6 + b 5 ⋅ 2 5 + b 4 ⋅ 2 4 + b 3 ⋅ 2 3 + b 2 ⋅ 2 2 + b 1 ⋅ 2 1 + b 0 ⋅ 2 0
然后利用乘法分配律分别计算每项与 f ( x ) f(x) f ( x ) G F ( 2 n ) GF(2^n) G F ( 2 n )