古典密码学概述

1. 隐写术 Steganography

隐写术是指首先用传统加密算法对数据进行加密，然后用某种方法将加密后的数据修改为一个伪装文本。

2. 替换密码 Substitution cipher

对数据中的每个字符用另一个字符进行替换。

  • 替换密码依赖与固定的替换结构
  • 对于字母表中的每一个字母的替换都是固定的

【注】

  1. 一次替换一个字符显然会在密文中留下太多的明文结构
  2. 如果已知明文的性质/结构，则可以通过统计攻击轻松破解任何替换密码

2.1 单字母单表密码 Monoalphabetic cipher

  • 凯撒密码 Caesar cipher
  1. 密钥 k∈{0,1,⋯ ,25}k \in \{0,1,\cdots,25\}，字母表 {a,b,⋯ ,z}\{a,b,\cdots,z\} 与集合 {0,1,⋯ ,25}\{0,1,\cdots,25\} 对应。
  • 明文空间 = 密文空间 = Σ+\Sigma^+（其中 Σ\Sigma 为字母表 {a,b,⋯ ,z}\{a,b,\cdots,z\}）
  • 密钥空间 = 2626
  1. 设密钥为 k=3k = 3，明文为 m=are you readym = are \ you \ ready，密文为 cc。则：
  • 加密

ci=Enc(mi,k)=(mi+3)  mod  26\begin{array}{c} c_i = Enc(m_i,k) = (m_i+3) \,\, mod \,\, 26 \end{array}

最终加密结果：

c=DUH BRX UHDGB\begin{array}{c} c = DUH \ BRX \ UHDGB \end{array}

  • 解密

mi=Dec(ci,k)=(ci−3)  mod  26\begin{array}{c} m_i = Dec(c_i,k) = (c_i-3) \,\, mod \,\, 26 \end{array}

最终解密结果：

m=are you ready\begin{array}{c} m = are \ you \ ready \end{array}

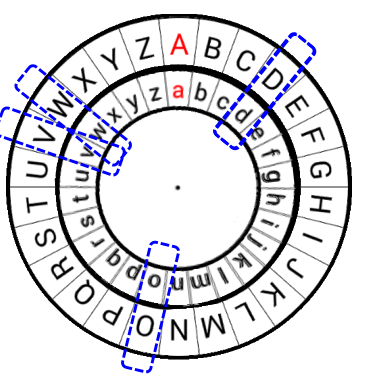
统计攻击方法

  • 原理：令 pip_i 指示在正常的英文内容中第 ii 个字符出现的频率。则有统计公式：

∑i=025pi2≈0.065\begin{array}{c} \sum_{i=0}^{25} p_i^2 \approx 0.065 \end{array}

  • 方法：
  1. 定义

Ij=∑i=025pi⋅qi+j\begin{array}{c} I_j = \sum_{i=0}^{25} p_i \cdot q_{i+j} \end{array}

其中，pip_i、qi+jq_{i+j} 分别是对应明文字母表第 ii 个字符的频率、密文字符表中第 i+ji+j 个字符的频率。

  1. 计算 j∈{0,1,⋯ ,25}j \in \{0,1,\cdots,25\} 对应的 IjI_j 的值。
  2. 选择 IjI_j 值接近 0.0650.065 的 jj 值输出，这些 jj 值很可能是密钥 kk 。
  3. 对于每一个可能的 jj 值，计算解密后的原文，看是否有实际意义，有则说明该 jj 值即密钥，无则说明不是。
  • Mixed alphabetic cipher
    字母表 {a,b,⋯ ,z}\{a,b,\cdots,z\} 到字母表 {A,B,⋯ ,Z}\{A,B,\cdots,Z\} 的映射是一个置换，每个小写字母（代表明文）分别映射到一个唯一的大写字母（表示密文）。
  1. 密钥空间 = 26!26!
  2. 每个字母的映射是固定的
  3. 已知语言中单个字母的概率分布
  • 摩斯码 Morse code
    每个字母映射为一系列点和短横线。

国际摩斯码

  1. 一条短横线等于三个点。
  2. 一个字母对应的系列点和短横线间的空格间隔等于一个点长度
  3. 两个相邻字母间的空格间隔等于三个点的长度
  4. 两个单词间的空格间隔等于七个点的长度

2.2 单字母多表密码 Polyalphabetic cipher

根据密钥中的元素，替换规则从一个字母位置到下一个字母位置会发生改变。相同的明文字符可以对应不同的密文字符。

  • 维吉尼亚密码
  1. 给定一定长度密钥，重复密钥直至密钥流和明文长度相同。
  2. 加密

ci=(mi+ki  mod  l)  mod  26\begin{array}{c} c_i = (m_i + k_{i \,\, mod \,\, l}) \,\, mod \,\, 26 \end{array}

  1. 解密

mi=(ci−ki mod l) mod 26\begin{array}{c} m_i = (c_i - k_{i \ mod \ l}) \ mod \ 26 \end{array}

  1. 根据加解密公式可以构造出表格法：
    假如明文为 asimpleexamplea simple example，密钥为 battistabattista，则表格法加密过程为：
  • 生成密钥流与明文字符一一对应：
Plaintext a s i m p l e e x a m p l e
Keystream b a t t i s t a b a t t i s
  • 参照表格（Tabula recta）计算密文。其中，明文字符对应行索引，密钥字符对应列索引：
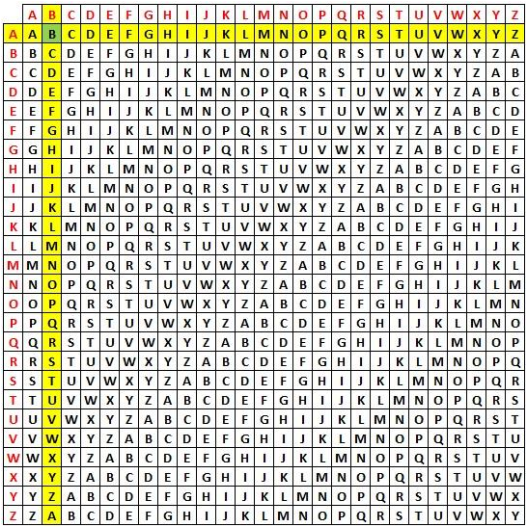
  • 最终计算得到的密文为：
Plaintext a s i m p l e e x a m p l e
Keystream b a t t i s t a b a t t i s
Ciphertext B S B F X D X E Y A F I T W
  • 解密过程就是加密的逆过程。根据密钥字符对应的列，寻找密文字符，则密文字符在表格中对应的行索引字符即明文字符。
  • 一次性密码本 OTP（One-time pad）
    OTP 是唯一一个达到完美加密的加密系统，无法被攻破。

要求

  1. OTP 的安全性完全取决于密钥的随机性，即密钥必须是随机产生的。
  2. 密钥长度必须大于等于明文长度。
  3. 密钥只能使用一次，不能重复使用。
  4. 密钥必须完全保密。

示例
比如要加密的消息为「This is an example」，用于加密的密钥（一次性密码本）为「MASKL NSFLD FKJPQ」。

  1. 将字母表 {a,b,⋯ ,z}\{a,b,\cdots,z\} 映射到数字集合 {0,1,⋯ ,25}\{0,1,\cdots,25\}。得到：
  • This is an example → 19 7 8 18 8 18 0 13 4 23 0 12 15 11 4
  • MASKL NSFLD FKJPQ → 12 0 18 10 11 13 18 5 11 3 5 10 9 15 16
  1. 二者依序相加并模 26 得到密文消息如下：
  • 5 7 0 2 19 5 18 18 15 0 5 22 24 0 20 → FHACTFSSPAFWYAU
  1. 解密即反向操作即可。

2.3 多字母单表密码 Multiple letter cipher

  • 波雷费密码 Playfair cipher
    Playfair 密码是首种双字母替换密码。

原理

  1. 选取一个 keyword 作为密钥，去除密钥中重复出现的字母，将密钥的字母逐个从左到右，从上到下加入 5×55 \times 5 的矩阵中，剩下的空间将未加入的英文字母依照 a−za-z 的顺序加入，将字母将 II 和 JJ 视为同一字符（或将 QQ 去除）。
  2. 将要加密的明文分成两个一组。若组内的字母相同，将X（或Q）插入两字母之间，重新分组（例如 HELLO 将分成 HE LX LO）。若剩下一个字，也加入X字。
  3. 在每组中，找出两个字母在矩阵中的地方。
  • 若两个字母不在同一直行或同一横列，在矩阵中找出另外两个字母，使这四个字母成为一个长方形的四个角（读取按行对应，即两个字母分别依次对应同行的那个字母）
  • 若两个字母在同一横行，取这两个字母右方的字母（若字母在最右方则取最左方的字母）。
  • 若两个字母在同一直列，取这两个字母下方的字母（若字母在最下方则取最上方的字母）。
  1. 新找到的两个字母就是原本的两个字母加密的结果。
  • 希尔密码 Hill cipher
    希尔密码是运用基本矩阵论原理的替换密码，一次性替换三字母。

原理

  1. 将字母表 {a,b,⋯ ,z}\{a,b,\cdots,z\} 映射到数字集合 {0,1,⋯ ,25}\{0,1,\cdots,25\}。
  2. 加密密钥是一个 3×33 \times 3 的可逆矩阵（如果不可逆则无法解密）：

K=[k11k12k13k21k22k23k31k31k33]\begin{array}{c} K = \left[ \begin{matrix} k_{11} & k_{12} & k_{13} \\ k_{21} & k_{22} & k_{23} \\ k_{31} & k_{31} & k_{33} \\ \end{matrix} \right] \end{array}

  1. 明文被排列为以下格式：

M=[m1m2m3]\begin{array}{c} M = \left[ \begin{matrix} m_1 \\ m_2 \\ m_3 \\ \end{matrix} \right] \end{array}

  1. 加密公式为：

C=[c1c2c3]=(K⋅M) mod 26=([k11k12k13k21k22k23k31k31k33]⋅[m1m2m3]) mod 26\begin{array}{c} C = \left[ \begin{matrix} c_1 \\ c_2 \\ c_3 \\ \end{matrix} \right] = (K \cdot M) \ mod \ 26 = (\left[ \begin{matrix} k_{11} & k_{12} & k_{13} \\ k_{21} & k_{22} & k_{23} \\ k_{31} & k_{31} & k_{33} \\ \end{matrix} \right] \cdot \left[ \begin{matrix} m_1 \\ m_2 \\ m_3 \\ \end{matrix} \right]) \ mod \ 26 \end{array}

  1. 解密公式为：

M=(K−1C) mod 26=(K−1KM) mod 26=M\begin{array}{c} M = (K^{-1}C) \ mod \ 26 = (K^{-1}KM) \ mod \ 26 = M \end{array}

3. 置换密码 Transposition cipher

对数据中的字符重新排列，但不改变它们本身。

  • 篱笆密码法 Rail Fence cipher
    明文由上至下顺序写上，当到达最低部时，再回头向上，一直重复直至整篇明文写完为止。然后，再往右顺序抄写一次，即得到密文。

示例

  1. 明文：WE ARE DISCOVERED. FLEE AT ONCE
  2. 篱笆密码法：
1
2
3
W . . . E . . . C . . . R . . . L . . . T . . . E
. E . R . D . S . O . E . E . F . E . A . O . C .
. . A . . . I . . . V . . . D . . . E . . . N . .
  1. 密文：WECRL TEERD SOEEF EAOCA IVDEN
  • Column Transposition cipher
    将明文按行顺序排列，超过行长则另起一行。密钥为一个置换，密钥长度决定行的长度。根据密钥指定的置换顺序，一列一列读取字符组在一起得到密文。

示例

  1. 密钥：4 3 1 2 5 6 7
  2. 明文：attack postponed until two am
  3. 置换：
4 3 1 2 5 6 7
a t t a c k p
o s t p o n e
d u n t i l t
w o a m x y z
  1. 密文：TTNAAPTMTSUOAODWCOIXKNLYPETZ

4. 转轮密码机 Rotor machine

属于单字母多表密码加密，每次转动输出一个密文后，转轮机内部布线发生改变，即改变了明文字符和密文字符之间的映射关系。

  • German Enigma
  • Allied Hagelin
  • Japanese Purple