1. 欧几里得距离

给定空间中两个点 ${(x_1,y_1)}$，${(x_2,y_2)}$；它们之间的欧几里得距离公式为：

$$\begin{array}{c} \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \end{array}$$

即两个点之间的直线距离。本质是向量的 2-范数。

2. 曼哈顿距离

给定空间中两个点 ${(x_1,y_1)}$，${(x_2,y_2)}$；它们之间的曼哈顿距离公式为：

$$\begin{array}{c} |x_1-x_2|+|y_1-y_2| \end{array}$$

即两个点之间的水平距离绝对值加上垂直距离的绝对值。本质是向量的 1-范数。
在平面上，从原点 $O$ 引出八条射线，相邻两射线角度均为 ${45^\circ}$，则将整个平面划分成 8 块区域，对于每一块区域内的点 ${B(x_1,y_1)}$，${C(x_2,y_2)}$满足：

• 若 ${|OB| \lt |OC|}$，则 ${|BC| \lt |OC|}$（曼哈顿距离），即连接 $O$、$B$、$C$ 三点的最短曼哈顿树为 ${O \rightarrow B \rightarrow C}$ 。

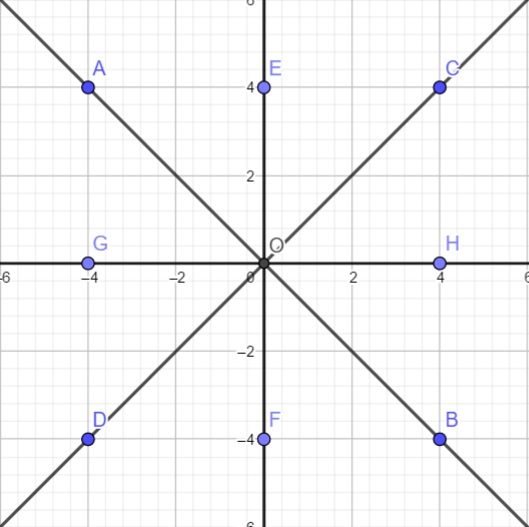
3. 切比雪夫距离

给定空间中两个点 ${(x_1,y_1)}$，${(x_2,y_2)}$；它们之间的切比雪夫距离公式为：

$$\begin{array}{c} max(|x_1-x_2|, |y_1-y_2|) \end{array}$$

即两点之间横纵坐标距离绝对值的最大值。本质是向量的 $\infty$-范数。

###【曼哈顿距离与切比雪夫距离比较】
如下图所示，矩形 ${EFGH}$ 是到原点曼哈顿距离为 2 的点的集合，矩形 ${ABCD}$ 是到原点切比雪夫距离为 2 的点的集合。

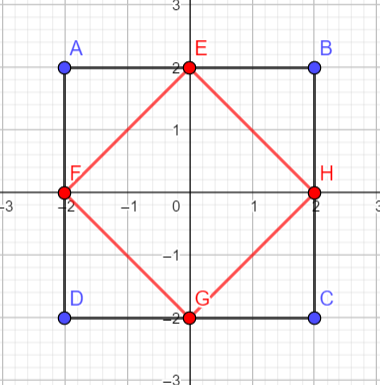
4. 闵可夫斯基距离

给定空间中两个点 ${(x_1,y_1)}$，${(x_2,y_2)}$；它们之间的闵可夫斯基距离公式为：

$$\begin{array}{c} \sqrt[p]{(x_1-x_2)^p+(y_1-y_2)^p} \end{array}$$

本质是向量的范数，$p$ 取不同的值时对应不同的 $p$-范数。